
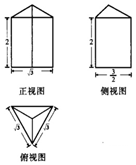
 如圖是由正三棱椎與正三棱柱組合而成的幾何體的三視圖,該幾何體的頂點都在半徑為R的球面上,則R=( )
如圖是由正三棱椎與正三棱柱組合而成的幾何體的三視圖,該幾何體的頂點都在半徑為R的球面上,則R=( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{1+\sqrt{2}}{2}$ | D. | $\sqrt{3}$ |
分析 幾何體外接球的球心在棱柱上下底面中心連線的中點,根據三棱柱的底面邊長和高,利用勾股定理即可求出外接球半徑.
解答  解:正三棱柱的底面邊長為$\sqrt{3}$,三棱柱的高為2,
解:正三棱柱的底面邊長為$\sqrt{3}$,三棱柱的高為2,
設正三棱柱的上下底面中心為O,O1,
則幾何體外接球的球心為OO1的中點H,
設三棱柱的底面一個頂點為A,
∵底面邊長為$\sqrt{3}$,∴O1A=$\frac{3}{2}×\frac{2}{3}$=1,O1H=1,
∴HA=$\sqrt{{O}_{1}{A}^{2}+{O}_{1}{H}^{2}}$=$\sqrt{2}$.
即外接球的半徑為$\sqrt{2}$.
故選:B.
點評 本題考查了棱柱與外接球的位置關系,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
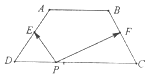 如圖,梯形ABCD中,AB∥CD,AB=2,CD=4,BC=AD=$\sqrt{5}$,E和F分別為AD與BC的中點,對于常數λ,在梯形ABCD的四條邊上恰好有8個不同的點P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立,則實數λ的取值范圍是( )
如圖,梯形ABCD中,AB∥CD,AB=2,CD=4,BC=AD=$\sqrt{5}$,E和F分別為AD與BC的中點,對于常數λ,在梯形ABCD的四條邊上恰好有8個不同的點P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立,則實數λ的取值范圍是( )| A. | (-$\frac{5}{4}$,-$\frac{9}{20}$) | B. | (-$\frac{5}{4}$,$\frac{11}{4}$) | C. | (-$\frac{1}{4}$,$\frac{11}{4}$) | D. | (-$\frac{9}{20}$,-$\frac{1}{4}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 30° | B. | 60° | C. | 150° | D. | 120° |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
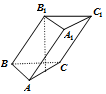 已知一三棱柱ABC-A1B1C1各棱長相等,B1在底面ABC上的射影是AC的中點,則異面直線AA1與BC所成角的余弦值為( )
已知一三棱柱ABC-A1B1C1各棱長相等,B1在底面ABC上的射影是AC的中點,則異面直線AA1與BC所成角的余弦值為( )| A. | $\frac{\sqrt{7}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com