Question

1．如圖，以A為原點建立空間直角坐標系A-xyz后，B（3，0，0），D（0，4，0），A₁（0，0，5），E（3，3，3），一質點從A點出發，沿直線向E點運動，然后會依次被長方體ABCD-A₁B₁C₁D₁的各個面反彈（符合反射定律），
反彈點依次記為E、F、G、…，
（Ⅰ） 求反彈點F的坐標；
（Ⅱ） 求質點到達第三個反彈點G時的運動距離；
（Ⅲ） 試判斷直線AE與直線FG的位置關系并證明你的結論．

Answer 1

分析 （Ⅰ）如圖所示，假設平面ABE與平面CDC₁D₁相交于MN，HE為法線．可得△AEH∽△EFM，可得MF．即可得出點F的坐標．
（Ⅱ）設反射光線與AN相交于點G．可得△GNF∽△EFM，可得NG．利用勾股定理可得：質點到達第三個反彈點G時的運動距離d=AE+EF+FG．
（Ⅲ）直線AE與直線FG的位置關系是AE∥FG．由（2）利用相似三角形的性質可得∠EAH=∠NGF，即可證明．

解答 解：（Ⅰ）如圖所示，假設平面ABE與平面CDC₁D₁相交于MN，HE為法線．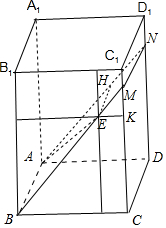
則△AEH∽△EFM，
AH=BE=3$\sqrt{2}$，EH=3=AB，EM=$\sqrt{2}$．
∴$\frac{AH}{EM}=\frac{HE}{MF}$，可得MF=1．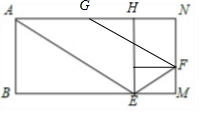
又MK=1，∴F（2，4，4）．
（Ⅱ）設反射光線與AN相交于點G．
則△GNF∽△EFM，
∴$\frac{NG}{EM}$=$\frac{NF}{MF}$，解得NG=2$\sqrt{2}$．
∴質點到達第三個反彈點G時的運動距離d=AE+EF+FG=$\sqrt{{3}^{2}+（3\sqrt{2}）^{2}}$+$\sqrt{{1}^{2}+（\sqrt{2}）^{2}}$+$\sqrt{{2}^{2}+（2\sqrt{2}）^{2}}$=6$\sqrt{3}$．
（Ⅲ）直線AE與直線FG的位置關系是AE∥FG．
證明如下：
由（2）可得：∠EAH=∠FEM=∠NGF，
∴AE∥FG．

點評 本題考查了空間位置關系、線面平行與垂直的判定及其性質定理、勾股定理、反射定理的應用、平行的判定與性質定理、相似三角形的判定與性質定理，考查了空間位置關系轉化為平面圖形的方法、空間想象能力、推理能力與計算能力，屬于難題．