
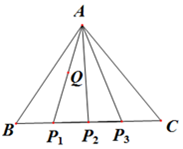
 設△ABC是邊長為1的正三角形,點P1,P2,P3四等分線段BC(如圖所示).
設△ABC是邊長為1的正三角形,點P1,P2,P3四等分線段BC(如圖所示).分析 (1)根據余弦定理和向量的數量積即可求出,
(2)根據向量的加減的幾何意義以及,向量的數量積,即可求出m的值,
(3)要使當$\overrightarrow{PA}•\overrightarrow{PC}$最小,則P必在線段P2C上,根據二次函數的性質即可求出.
解答 解:(1)原式=$\overrightarrow{A{P_1}}•(\overrightarrow{AB}+\overrightarrow{A{P_2}})=2{\overrightarrow{A{P_1}}^2}$,
在△ABP1中,由余弦定理,得$A{P_1}^2=1+\frac{1}{16}-2×1×\frac{1}{4}×cos{60^0}=\frac{13}{16}$,
所以$\overrightarrow{AB}•\overrightarrow{A{P_1}}+\overrightarrow{A{P_1}}•\overrightarrow{A{P_2}}$=$\frac{13}{8}$;
(2)易知$\overrightarrow{B{P_1}}=\frac{1}{4}\overrightarrow{BC}$,即$\overrightarrow{A{P_1}}-\overrightarrow{AB}=\frac{1}{4}(\overrightarrow{AC}-\overrightarrow{AB})$,即$\overrightarrow{A{P_1}}=\frac{3}{4}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$,
因為Q為線段AP1上一點,
設$\overrightarrow{AQ}=λ\overrightarrow{AP}=\frac{3}{4}λ\overrightarrow{AB}+\frac{1}{4}λ\overrightarrow{AC}=m\overrightarrow{AB}+\frac{1}{12}\overrightarrow{AC}$,
所以$m=\frac{1}{4}$;
(3)①當P在線段BP2上時(不含P2),此時$\overrightarrow{PA}•\overrightarrow{PC}$>0,
②當P在線段P2C上時(不含P2),$\overrightarrow{PA}•\overrightarrow{PC}$≤0,
要使當$\overrightarrow{PA}•\overrightarrow{PC}$最小,則P必在線段P2C上,
設$|{\overrightarrow{PC}}|=x$,由于AP2⊥BC,則$\overrightarrow{PA}•\overrightarrow{PC}=|{\overrightarrow{PA}}|•|{\overrightarrow{PC}}|cos∠APC$=|$\overrightarrow{PC}$|2•(-|$\overrightarrow{P{P}_{2}}$|)=x(x-$\frac{1}{2}$)=x2-$\frac{1}{2}$x
當$x=\frac{1}{4}$時,即當P為P3時,$\overrightarrow{PA}•\overrightarrow{PC}$最小,此時 由余弦定理可求得$cos∠PAB=\frac{5}{26}\sqrt{13}$
點評 本題主要考查兩個向量的數量積的運算,二次函數的性質,余弦定理,體現了轉化的數學思想,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | π | C. | -π | D. | 沒有正確答案 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| 廣告費用x(萬元) | 4 | 2 | 3 | 5 |
| 銷售額y(萬元) | 49 | 26 | 39 | 54 |
| A. | 63.6 萬元 | B. | 65.5 萬元 | C. | 67.7 萬元 | D. | 72.0 萬元 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com