
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 由復數代數形式的乘除運算化簡復數z,求出$\overline{z}$,再求出$\overline z$在復平面內對應的點的坐標,則答案可求.
解答 解:∵$z=\frac{i^3}{i-1}$=$\frac{-i(-1-i)}{(-1+i)(-1-i)}=\frac{-1+i}{2}=-\frac{1}{2}+\frac{1}{2}i$,
∴$\overline{z}=-\frac{1}{2}-\frac{1}{2}i$,
則其共軛復數$\overline z$在復平面內對應的點的坐標為:($-\frac{1}{2}$,-$\frac{1}{2}$),位于第三象限.
故選:C.
點評 本題考查了復數代數形式的乘除運算,考查了復數的代數表示法及其幾何意義,是基礎題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:選擇題
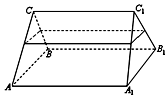 如圖,一個三棱柱形容器中盛有水,且側棱AA1=8.若側面AA1B1B水平放置時,液面恰好過AC,BC,A1C1,B1C1的中點.則當底面ABC水平放置時,液面高為( )
如圖,一個三棱柱形容器中盛有水,且側棱AA1=8.若側面AA1B1B水平放置時,液面恰好過AC,BC,A1C1,B1C1的中點.則當底面ABC水平放置時,液面高為( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
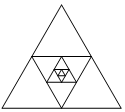 如圖,畫一個邊長為2的正三角形,再將這個正三角形各邊的中點相連得到第二個正三角形,依此類推,一共畫了5個正三角形.那么這五個正三角形的面積之和等于( )
如圖,畫一個邊長為2的正三角形,再將這個正三角形各邊的中點相連得到第二個正三角形,依此類推,一共畫了5個正三角形.那么這五個正三角形的面積之和等于( )| A. | 2$\sqrt{3}$ | B. | $\frac{21}{16}$$\sqrt{3}$ | C. | $\frac{85}{64}$$\sqrt{3}$ | D. | $\frac{341}{256}$$\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 2 | C. | -2 | D. | 6 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com