
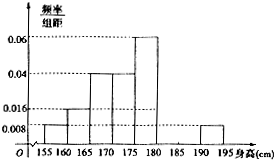
 從某學校的800名男生中隨機抽取50名測量身高,被測學生身高全部介于155cm和195cm之間,將測量結果按如下方式分成八組:第一組[155,160),第二組[160,165),…,第八組[190,195],下圖是按上述分組方法得到的頻率分布直方圖的一部分,已知第一組與第八組人數相同,第六組的人數為4人.
從某學校的800名男生中隨機抽取50名測量身高,被測學生身高全部介于155cm和195cm之間,將測量結果按如下方式分成八組:第一組[155,160),第二組[160,165),…,第八組[190,195],下圖是按上述分組方法得到的頻率分布直方圖的一部分,已知第一組與第八組人數相同,第六組的人數為4人.分析 (1)先由第六組的人數除以樣本容量得到第六組的頻率,然后用1減去出第七組外各組的頻率和即可得到第七組的頻率;因為過中位數的直線兩側的矩形的面積相等,經計算前三組的頻率和小于0.5,后四組的頻率和大于0.5,由此斷定中位數位于第四組,設出中位數m,由0.04+0.08+0.2+(m-170)×0.04=0.5即可求得中位數m的值;
(2)分別求出第六組和第八組的人數,利用列舉法列出從身高屬于第六組和第八組的所有男生中隨機抽取兩名男生的總的方法,再根據古典概型的概率公式解之即可.
解答 解:(1)第六組的頻率為$\frac{4}{50}=0.08$,…1分
第七組的頻率為1-0.08-5×(0.08×2+0.016+0.04×2+0.06)=0.06…(3分)
易知中位數位于[170,175]之間設為m,則有(m-170)×0.04=0.5-0.32=0.18,m=174.5
身高在180cm以上(含180cm)的人數為0.18×800=144人…(6分)
(2)第六組[180,185)的人數為4人,設為a,b,c,d,
第八組[190,195]的人數為2人,設為A,B,
則從中抽取兩人有ab,ac,ad,bc,bd,cd,aA,bA,cA,dA,aB,bB,cB,dB,AB共15種情況,
因事件E={|x-y|≤5}發生當且僅當隨機抽取的兩名男生在同一組,
所以事件E包含的基本事件為ab,ac,ad,bc,bd,cd,AB共7種情況,
故$P=\frac{7}{15}$…(12分)
點評 本題考查了頻率分布直方圖,考查了列舉法求基本事件及事件發生的概率,解答此題的關鍵是明確頻率直方圖中各矩形的頻率和等于1,中位數是頻率分布直方圖中,過該點的直線把各矩形面積均分的點的橫坐標,此題是基礎題.


 名題金卷系列答案
名題金卷系列答案 優加精卷系列答案
優加精卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1條 | B. | 2條 | C. | 3條 | D. | 4條 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
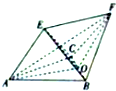 如圖所示,在多面體EF-ABC中,△ABC是邊長為2的等邊三角形,O為BC的中點,EF∥AO,EA=EC=EF=$\sqrt{3}$.
如圖所示,在多面體EF-ABC中,△ABC是邊長為2的等邊三角形,O為BC的中點,EF∥AO,EA=EC=EF=$\sqrt{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | r>$\frac{1}{2}$ | B. | $\frac{1}{2}$<r<$\frac{3}{2}$ | C. | r<$\frac{3}{2}$ | D. | r≥$\frac{3}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com