
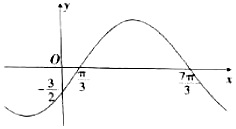
 已知函數$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|<\frac{π}{2}})$的部分圖象如圖所示,將函數y=f(x)的圖象向左平移$\frac{4π}{3}$個單位,得到函數y=g(x)的圖象,則函數y=g(x)在區間$[{\frac{π}{2},\frac{5π}{2}}]$上的最大值為( )
已知函數$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|<\frac{π}{2}})$的部分圖象如圖所示,將函數y=f(x)的圖象向左平移$\frac{4π}{3}$個單位,得到函數y=g(x)的圖象,則函數y=g(x)在區間$[{\frac{π}{2},\frac{5π}{2}}]$上的最大值為( )| A. | 3 | B. | $\frac{{3\sqrt{3}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 利用函數的圖象求出T,利用周期公式求出ω,利用函數的圖象經過的特殊點,集合φ的范圍,求出φ得到函數的解析式,進而可求g(x)解析式,利用正弦函數的性質即可得解.
解答 解:由圖象可知T=4π,從而ω=$\frac{1}{2}$,
將($\frac{π}{3}$,0),(0,-$\frac{3}{2}$)在函數圖象上,$\left\{\begin{array}{l}{Asin(\frac{π}{6}+φ)=0}\\{Asinφ=-\frac{3}{2}}\end{array}\right.$,|φ|<$\frac{π}{2}$,
可得:φ=-$\frac{π}{6}$,A=3,f(x)=3sin($\frac{1}{2}x$-$\frac{π}{6}$),
可得:g(x)=3sin[$\frac{1}{2}$(x+$\frac{4π}{3}$)-$\frac{π}{6}$]=3cos$\frac{1}{2}x$.
由x∈$[{\frac{π}{2},\frac{5π}{2}}]$,可得:$\frac{1}{2}x$∈[$\frac{π}{4}$,$\frac{5π}{4}$],
可得:3cos$\frac{1}{2}x$∈[-3,$\frac{3\sqrt{2}}{2}$].
故選:C.
點評 本題考查由y=Asin(ωx+φ)的部分圖象確定其解析式,函數y=Asin(ωx+φ)的圖象變換,考查計算能力,屬于基礎題.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:高中數學 來源: 題型:選擇題
| A. | 14 | B. | 15 | C. | 14或15 | D. | 15或16 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
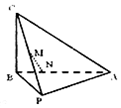 如圖,在三棱錐C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,點M是PC的中點,點N在線段AB上,且MN⊥AB.
如圖,在三棱錐C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,點M是PC的中點,點N在線段AB上,且MN⊥AB.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
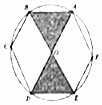 已知正六邊形ABCDEF內接于圓O,連接AD,BE,現在往圓O內投擲2000粒小米,則可以估計落在陰影區域內的小米的粒數大致是( )(參考數據:$\frac{π}{\sqrt{3}}$=1.82,$\frac{\sqrt{3}}{π}$=0.55)
已知正六邊形ABCDEF內接于圓O,連接AD,BE,現在往圓O內投擲2000粒小米,則可以估計落在陰影區域內的小米的粒數大致是( )(參考數據:$\frac{π}{\sqrt{3}}$=1.82,$\frac{\sqrt{3}}{π}$=0.55)| A. | 550 | B. | 600 | C. | 650 | D. | 700 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,1] | B. | (-∞,-1] | C. | [-1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
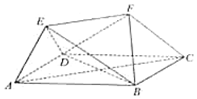 如圖,在多面體ABCDEF中,底面ABCD是菱形,AB=2,∠DAB=60°,EF∥AC,EF=$\sqrt{3}$.
如圖,在多面體ABCDEF中,底面ABCD是菱形,AB=2,∠DAB=60°,EF∥AC,EF=$\sqrt{3}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com