
 如右圖所示,已知正方形
如右圖所示,已知正方形 和矩形
和矩形 所在的平面互相垂直,
所在的平面互相垂直,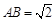 ,AF = 1,M是線段
,AF = 1,M是線段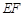 的中點.
的中點.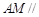 平面
平面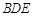 ;
;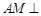 平面
平面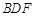 ;
;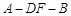 的大小.
的大小.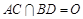 ,連結(jié)EO
,連結(jié)EO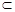 面BDE,AM
面BDE,AM 面BDE
面BDE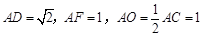 ,知四邊形AOMF為正方形
,知四邊形AOMF為正方形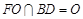
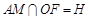 ,作HG⊥DF于G,連結(jié)AG,由三垂線定理知AG⊥DF
,作HG⊥DF于G,連結(jié)AG,由三垂線定理知AG⊥DF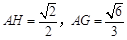 ···················· 12分
···················· 12分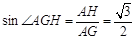
 ··················· 13分
··················· 13分

 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
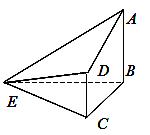
 中,
中,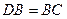 ,
, 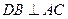 ,點
,點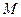 是棱
是棱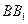 上一點.
上一點.
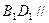 面
面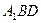 ;
;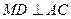 ;
;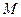 的位置,使得平面
的位置,使得平面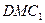
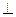 平面
平面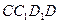 .
.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
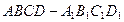 中(側(cè) 棱與底面垂直的四棱柱),
中(側(cè) 棱與底面垂直的四棱柱),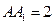 ,底面是邊長為
,底面是邊長為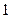 的正方形,
的正方形,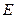 、
、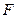 、
、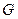 分別是棱
分別是棱 、
、 、
、 的中點
的中點
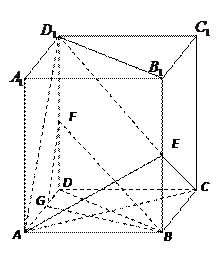
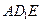
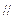 平面
平面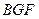 ;
;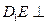 面
面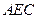 。
。查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
 中,
中,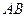 ⊥平面
⊥平面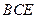 ,
,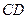 ⊥平面
⊥平面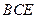 ,
,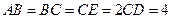 ,
,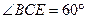 .
. 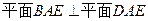 ;
;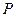 為線段
為線段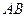 上一點,求直線
上一點,求直線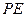 與平面
與平面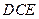 所成角的取值范圍.
所成角的取值范圍.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
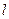 、
、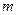 、
、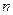 是互不相同的空間直線,
是互不相同的空間直線,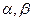 是不重合的平面,則下列命題中為真命題的是( )
是不重合的平面,則下列命題中為真命題的是( )A.若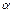 ∥β, ∥β,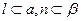 ,則 ,則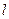 ∥n ∥n | B.若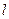 ⊥ ⊥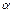 , , 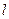 ∥β,則 ∥β,則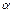 ⊥β ⊥β |
C.若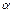 ⊥β, ⊥β,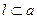 ,則 ,則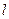 ⊥β ⊥β | D.若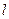 ⊥n,m⊥n,則 ⊥n,m⊥n,則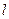 ∥m ∥m |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
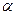 、
、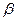 、
、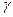 是三個不同的平面,a、b是兩條不同的直線,給出下列4個命題:
是三個不同的平面,a、b是兩條不同的直線,給出下列4個命題: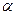 ,b∥
,b∥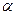 ,則a∥b; ②若a∥
,則a∥b; ②若a∥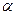 ,b∥
,b∥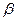 ,a∥b,則
,a∥b,則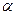 ∥
∥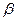 ;③若a⊥
;③若a⊥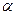 ,b⊥
,b⊥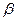 ,a⊥b,則
,a⊥b,則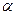 ⊥
⊥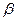 ;④若a、b在平面
;④若a、b在平面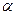 內(nèi)的射影互相垂直,則a⊥b. 其中正確命題是( )
內(nèi)的射影互相垂直,則a⊥b. 其中正確命題是( )| A.③ | B.④ | C.①③ | D.②④ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
A.(0, ) ) | B.(1,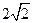 ) ) |
C.(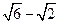 , , ) ) | D.(0,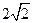 ) ) |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com