
分析 設P(x0,y0),I(x1,y1),則G($\frac{{x}_{0}}{3},\frac{{y}_{0}}{3}$),由已知條件推導出a=2c,b=$\frac{|-3\sqrt{2}|}{\sqrt{(\sqrt{2})^{2}+(-1)^{2}}}$=$\sqrt{6}$,結合隱含條件求得a2,則橢圓方程可求.
解答 解:設P(x0,y0),I(x1,y1),則G($\frac{{x}_{0}}{3},\frac{{y}_{0}}{3}$).
又IG∥F1F2,yI=$\frac{{y}_{0}}{3}$,|F1F2|=2c,
∴${S}_{△{F}_{1}P{F}_{2}}$=$\frac{1}{2}$•|F1F2|•|y0|=$\frac{1}{2}$(|F1F2|+|PF1|+|PF2|)•|$\frac{{y}_{0}}{3}$|,
∴2c=$\frac{2a+2c}{3}$,故a=2c.
又直線$y=\sqrt{2}x-3\sqrt{2}$與以原點為圓心,以橢圓C的短半軸為半徑的圓相切,
∴b=$\frac{|-3\sqrt{2}|}{\sqrt{(\sqrt{2})^{2}+(-1)^{2}}}$=$\sqrt{6}$,
∴${a}^{2}=6+\frac{{a}^{2}}{4}$,得a2=8.
∴橢圓C的標準方程為$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{6}=1$.
故答案為:$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{6}=1$.
點評 本題考查橢圓方程的求法,考查直線與圓的位置關系,考查學生分析解決問題的能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(2x)min=f(0) | B. | f(2x)max=f(0) | ||
| C. | f(2x)在(-∞,+∞)上遞減,無極值 | D. | f(2x)在(-∞,+∞)上遞增,無極值 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
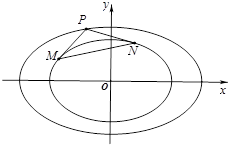 已知橢圓${C_1}:\frac{x^2}{2}+{y^2}=1$
已知橢圓${C_1}:\frac{x^2}{2}+{y^2}=1$查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-2)∪(0,2) | B. | (-∞,-2)∪(2,+∞) | C. | (-2,0)∪(2,+∞) | D. | (-2,0)∪(0,2) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com