
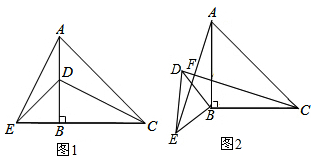
分析 (1)延長CD交AE于K,根據全等三角形的性質得到AE=CD,∠EAB=∠DCB,由于∠DCB+∠CDB=90°,于是得到結論;
(2)由于∠DBE=∠ABC=90°,得到∠ABE=∠DBC,根據全等三角形的性質得到AE=CD,∠EAB=∠DCB,等量代換得到∠KOA+∠KAO=90°,于是得到結論.
解答  解:(1)AE=CD,AE⊥CD,
解:(1)AE=CD,AE⊥CD,
理由:延長CD交AE于F,
在△AEB和△CDB中,
∵$\left\{\begin{array}{l}{∠ABE=∠CBD=90°}\\{AB=BC}\\{BE=DB}\end{array}\right.$,
∴△AEB≌△CDB(SAS)
∴AE=CD,
∠EAB=∠DCB,
∵∠DCB+∠CDB=90°,
∠ADF=∠CDB,
∴∠ADF+∠DAF=90°,
∴∠AFD=90°,
∴AE⊥CD;
(2)解:(2)AE=CD,AE⊥CD,
∵∠DBE=∠ABC=90°,
∴∠ABE=∠DBC,
在△AEB和△CDB中,$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠DBC}\\{BE=BD}\end{array}\right.$
∴△AEB≌△CDB,
∴AE=CD,∠EAB=∠DCB,
∵∠DCB+∠COB=90°,∠AOK=∠COB,
∴∠KOA+∠KAO=90°,
∴∠AKC=90°,
∴AE⊥CD.
點評 此題考查了全等三角形的判定與性質,用到的知識點全等三角形的判定與性質,關鍵是能在較復雜的圖形中找出全等的三角形.


 黎明文化寒假作業系列答案
黎明文化寒假作業系列答案 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 平均數是15 | B. | 眾數是10 | C. | 中位數是17 | D. | 方差是$\frac{44}{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
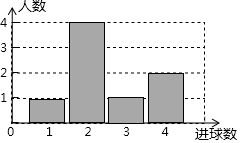 體育課上,老師為了解女學生定點投籃的情況,隨機抽取8名女生進行每人4次定點投籃的測試,進球數的統計如圖所示.
體育課上,老師為了解女學生定點投籃的情況,隨機抽取8名女生進行每人4次定點投籃的測試,進球數的統計如圖所示.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
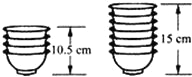 如圖,兩摞規格相同的碗整齊地疊放在桌面上,請根據圖中給出的數據信息,解答下列問題:
如圖,兩摞規格相同的碗整齊地疊放在桌面上,請根據圖中給出的數據信息,解答下列問題:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com