
 如圖,在△ABC中,AB=AC,點E在CA延長線上,EP⊥BC于點P,交AB于點F,若AF=2,BF=3,則CE的長度為( )
如圖,在△ABC中,AB=AC,點E在CA延長線上,EP⊥BC于點P,交AB于點F,若AF=2,BF=3,則CE的長度為( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 根據(jù)△ABC中,AB=AC,EP⊥BC,可以得到∠E=∠EFA,然后根據(jù)角相等得出邊相等即可求得答案.
解答 解:∵在△ABC中,AB=AC,點E在CA延長線上,EP⊥BC于點P,交AB于點F,
∴∠B=∠C,∠BPE=∠EPC=90°,
∴在直角△BPF和直角△EPC中有:∠BFP=∠E,
又∵∠BFP=∠EFA,
∴∠E=∠EFA,
∴AE=AF,
又∵AF=2,BF=3,
AB=AC=AF+BF=2+3=5,AE=AF=2,
∴CE=AE+AC=5+2=7,
故選:C.
點評 此題是等腰三角形的性質,主要考查了等腰三角形的性質,直角三角形的性質,解本題的關鍵是靈活運用等腰三角形的性質.


科目:初中數(shù)學 來源: 題型:解答題
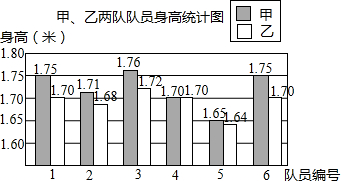 某校要成立一支由6名女生組成的舞蹈隊,初三(1)、(2)班各選6名女生,分別組成甲隊和乙隊參加選拔,每位女生的身高(cm)統(tǒng)計如圖,部分統(tǒng)計量如表:(單位:米)
某校要成立一支由6名女生組成的舞蹈隊,初三(1)、(2)班各選6名女生,分別組成甲隊和乙隊參加選拔,每位女生的身高(cm)統(tǒng)計如圖,部分統(tǒng)計量如表:(單位:米) | 平均數(shù) | 標準差 | 中位數(shù) | |
| 甲隊 | 1.72 | 0.038 | 1.73 |
| 乙隊 | 1.69 | 0.025 | 1.70 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
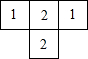 由6個小立方體組成的幾何體的俯視圖如圖1所示,每個小正方形上的數(shù)字表示該位置上擺放的小立方體的個數(shù),則該幾何體的左視圖應為( )
由6個小立方體組成的幾何體的俯視圖如圖1所示,每個小正方形上的數(shù)字表示該位置上擺放的小立方體的個數(shù),則該幾何體的左視圖應為( )| A. | 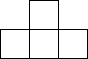 | B. | 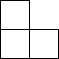 | C. | 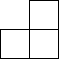 | D. | 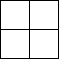 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
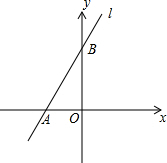 如圖,直線l與x軸相交于點A(-2,0),與y軸相交于點B,∠BAO=60°.
如圖,直線l與x軸相交于點A(-2,0),與y軸相交于點B,∠BAO=60°.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
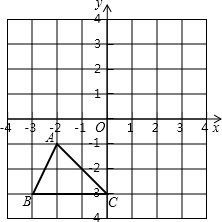 如圖,在方格紙中,已知格點△ABC和格點O.
如圖,在方格紙中,已知格點△ABC和格點O.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
 如圖,已知平行四邊形ABCD,下列四個條件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD從中選兩個作為補充條件,使它成為正方形,其中錯誤的是( )
如圖,已知平行四邊形ABCD,下列四個條件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD從中選兩個作為補充條件,使它成為正方形,其中錯誤的是( )| A. | ①② | B. | ②③ | C. | ①③ | D. | ②④ |
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com