
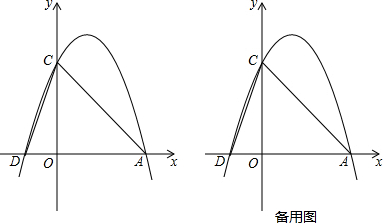
分析 (1)將x=0代入拋物線的解析式得y=3,從而得到C(0,3),將點C的坐標代入y=-x+n得到:n=3,于是可求得y=-x+3,令y=0得到-x+3=0,解得x=3,故此可知A(3,0),將點A的坐標代入拋物線的解析式求得b=2,可得到拋物線的解析式為y=-x2+2x+3;
(2)如圖1所示:令y=0可求得點D的坐標為(-1,0),依據待定系數法可求得直線DC的解析式為y=3x+3,由PE∥DC可知直線PE的一次項系數為3,設直線PE的解析式為y=3x+b1.由E在AC上可知點E的坐標為(t,-t+3),將點E的坐標代入y=3x+b1可求得:b1=3-4t,于是可求得直線PE的解析式為y=3x+3-4t,將x=m代入直線的解析式得:y=3m+3-4t,將x=m代入拋物線的解析式得:y=-m2+2m+3.于是可得到-m2+2m+3=3m+3-4t,從而可得到t=$\frac{1}{4}{m}^{2}+\frac{1}{4}m$;
(3)如圖2所示:點E的坐標為(t,-t+3),點P的坐標為(m,3m+3-4t).①當PC=PE時.由兩點間的距離公式可知m2+(3m-4t)2=(m-t)2+(3m-3t)2.整理得:m=$\frac{3}{2}$5t.將m=$\frac{3}{2}$t代入t=$\frac{1}{4}{m}^{2}+\frac{1}{4}m$可求得t=$\frac{10}{9}$;②當PC=EC時.由兩點間的距離公式可知:m2+(3m-4t)2=t2+(-t+3-3)2.從而可求得m=$\frac{7}{5}t$,將m=$\frac{7}{5}t$代入t=$\frac{1}{4}{m}^{2}+\frac{1}{4}m$可求得t=$\frac{65}{49}$.
解答 解:(1)∵y=-x2+bx+3與y軸交于點C,
∴點C的坐標為(0,3).
∵將點C的坐標代入y=-x+n得到:n=3,
∴直線AC的解析式為y=-x+3.
∵將y=0代入得:-x+3=0,解得x=3,
∴點A的坐標為(3,0).
將點A的坐標代入拋物線的解析式得:-9+3b+3=0.
解得:b=2.
∴拋物線的解析式為y=-x2+2x+3.
(2)如圖1所示: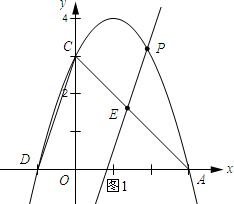
∵令y=0得:-x2+2x+3=0.解得:x1=-1,x2=3,
∴點D的坐標為(-1,0).
設直線DC的解析式為y=kx+b,將點D、C的解析式代入$\left\{\begin{array}{l}{b=3}\\{-k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=3}\\{b=3}\end{array}\right.$.
∴直線DC的解析式為y=3x+3.
∵PE∥DC,
∴直線PE的一次項系數為3.
∵點E的橫坐標為t,點E在直線AC上,
∴點E的縱坐標為-t+3.
∴點E的坐標為(t,-t+3)
設直線PE的解析式為y=3x+b1.將點E的坐標代入直線的解析式得:3t+b1=-t+3.
解得:b1=3-4t.
∴直線PE的解析式為y=3x+3-4t.
將x=m代入直線的解析式得:y=3m+3-4t,將x=m代入拋物線的解析式得:y=-m2+2m+3.
∴-m2+2m+3=3m+3-4t.
整理得:t=$\frac{1}{4}{m}^{2}+\frac{1}{4}m$(0<m<3).
(3)如圖2所示:
①當PC=PE時.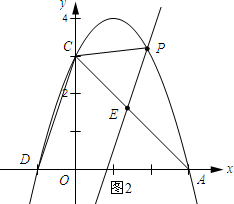
由(2)可知點E的坐標為(t,-t+3),點P的坐標為(m,3m+3-4t).
∵PC=PE,
∴m2+(3m-4t)2=(m-t)2+(3m-3t)2.整理得:m=$\frac{3}{2}$5t.
將m=$\frac{3}{2}$t代入t=$\frac{1}{4}{m}^{2}+\frac{1}{4}m$得;t=$\frac{1}{4}×(\frac{3}{2}t)^{2}$+$\frac{1}{4}×\frac{3}{2}t$,整理得:$\frac{9}{16}{t}^{2}-\frac{5}{8}t=0$.
解得:t1=$\frac{10}{9}$,t2=0(舍去).
②當PC=EC時.
由兩點間的距離公式可知:m2+(3m-4t)2=t2+(-t+3-3)2.整理得:5m2-12mt+7t2=0.
∴(m-t)(5m-7t)=0.
∵m≠t,
∴5m=7t,即m=$\frac{7}{5}t$
將m=$\frac{7}{5}t$代入t=$\frac{1}{4}{m}^{2}+\frac{1}{4}m$得;t=$\frac{1}{4}×(\frac{7}{5}t)^{2}$+$\frac{1}{4}×\frac{7}{5}t$,整理得:$\frac{49}{100}{t}^{2}-\frac{13}{20}t$=0.
解得:t1=$\frac{65}{49}$,t2=0(舍去).
綜上所述,t的值為$\frac{10}{9}$或$\frac{65}{49}$.
點評 本題主要考查的是二次函數的綜合應用,解答本題主要應用了待定系數法求一次函數、二次函數的解析式,、兩點間的距離公式,求得點E和點P的坐標,并利用兩點間的距離公式列出t與m的方程是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
 《九章算術》是中國傳統數學最重要的著作,奠定了中國傳統數學的基本框架.它的代數成就主要包括開方術、正負術和方程術.其中,方程術是《九章算術》最高的數學成就.《九2x=-6章算術》中記載:“今有人共買雞,人出九,盈十一;人出六,不足十六.問人數、雞價各幾何?”
《九章算術》是中國傳統數學最重要的著作,奠定了中國傳統數學的基本框架.它的代數成就主要包括開方術、正負術和方程術.其中,方程術是《九章算術》最高的數學成就.《九2x=-6章算術》中記載:“今有人共買雞,人出九,盈十一;人出六,不足十六.問人數、雞價各幾何?”| A. | 9x+11=6x-16 | B. | 9x-11=6x+16 | C. | $\frac{x-11}{9}=\frac{x+16}{6}$ | D. | $\frac{x+11}{9}=\frac{x-16}{6}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
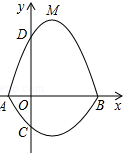 如圖,在平面直角坐標系xOy中,A、B為x軸上兩點,C、D為y軸上的兩點,經過點A、C、B的拋物線的一部分C1與經過點A、D、B的拋物線的一部分C2組合成一條封閉曲線,我們把這條封閉曲線成為“蛋線”.已知點C的坐標為(0,-$\frac{3}{2}$),點M是拋物線C2:y=mx2-2mx-3m(m<0)的頂點.
如圖,在平面直角坐標系xOy中,A、B為x軸上兩點,C、D為y軸上的兩點,經過點A、C、B的拋物線的一部分C1與經過點A、D、B的拋物線的一部分C2組合成一條封閉曲線,我們把這條封閉曲線成為“蛋線”.已知點C的坐標為(0,-$\frac{3}{2}$),點M是拋物線C2:y=mx2-2mx-3m(m<0)的頂點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
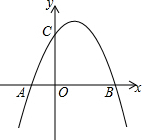 如圖,已知c>0,拋物線y=-x2+bx+c與x軸交于A(x1,0),B(x2,0)兩點(x2>x1),與y軸交于點C.
如圖,已知c>0,拋物線y=-x2+bx+c與x軸交于A(x1,0),B(x2,0)兩點(x2>x1),與y軸交于點C.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com