
分析 先變形為$\sqrt{{x}^{2}+7}$=$\sqrt{2}x$+1,兩邊平方得到x2+7=2x2+2$\sqrt{2x}$+1,再變形,利用配方法即可解答此無理方程.
解答 解:∵$\sqrt{{x}^{2}+7}$-$\sqrt{2}x$=1,
∴$\sqrt{{x}^{2}+7}$=$\sqrt{2}x$+1,
∴x2+7=2x2+2$\sqrt{2}$x+1
∴x2+2$\sqrt{2}$x-6=0
∴$(x+\sqrt{2})^{2}$=8,
∴$x+\sqrt{2}=±2\sqrt{2}$,
∴x=$-\sqrt{2}±2\sqrt{2}$,
∴${x}_{1}=-3\sqrt{2}$,${x}_{2}=\sqrt{2}$
點評 此題考查了解無理方程,解無理方程關鍵是要去掉根號,將其轉化為整式方程.解無理方程的基本思想是把無理方程轉化為有理方程來解,在變形時要注意根據方程的結構特征選擇解題方法.


 品學雙優卷系列答案
品學雙優卷系列答案 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
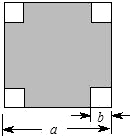 如圖,在一塊邊長為acm的正方形紙板的四角,各剪去一個邊長為bcm的正方形(b<$\frac{a}{2}$),列出表示剩余部分面積的代數式,然后利用因式分解計算當a=13.2,b=3.4時,剩余部分的面積.
如圖,在一塊邊長為acm的正方形紙板的四角,各剪去一個邊長為bcm的正方形(b<$\frac{a}{2}$),列出表示剩余部分面積的代數式,然后利用因式分解計算當a=13.2,b=3.4時,剩余部分的面積.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
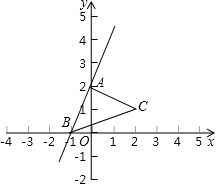 在平面直角坐標系中,點A,B,C的坐標分別為(0,2),(-1,0),(2,1).
在平面直角坐標系中,點A,B,C的坐標分別為(0,2),(-1,0),(2,1).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com