Question

3．如圖，一菜地為直角三角形ABC，有∠BAC=90°，AC=60米，AB=80米，BC邊為一小河，現在需要將菜地平均分配，且每一塊地都面臨小河以方便取水灌溉．
（1）試在圖1，圖2中，用兩種不同方案畫出等分成兩部分的分割線，并分別求出分割線的長度．
（2）試在圖3中畫出分割線（需必要的說明），并求出該分割線的總長度，要求：①分成三部分面積相等；②為減少土地損失，分割線總長度要求最小．

Answer 1

分析 （1）先根據勾股定理求斜邊BC=100米，再求S_△ABC=2400米²；如圖1，考慮面積一半為1200米²，令一邊BD=60米，過D作AC的平行線，交BC于E，根據相似得DE=40米，則S_△BDE=$\frac{1}{2}$S_△ABC，且割線DE=40米；如圖2，根據三角形中線的性質平分三角形面積，即可得出作法，求出即可．
（2）如圖3中，分割線分別為EF、MN，當BE=BF，CM=CN，S_△BEF=S_△CMN=800時，分割線之和最小．利用相似三角形的性質分別求解即可．

解答 解：（1）∵∠BAC=90°，AC=60米，AB=80米，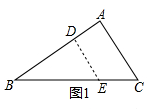
由勾股定理得：BC=$\sqrt{6{0}^{2}+8{0}^{2}}$=100米，
如圖1，根據相似三角形面積比是相似比的平方，我們可以過直角邊AB上一點D，作平行于另一直角邊的直線，將三角形分成兩部分，面積相等，邊長比為1：$\sqrt{2}$，
∵DE∥AC，
∴△BDE∽△BAC
∴$\frac{DE}{AC}=\frac{BD}{AB}$=$\frac{1}{\sqrt{2}}$，
∴$\frac{BD}{80}$=$\frac{1}{\sqrt{2}}$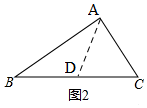
如圖2，取BC的中點，連接AD，則BD=CD，
根據等底同高的兩個三角形面積相等，得：S_△ABD=S_△ADC；
AD=$\frac{1}{2}$BC=$\frac{1}{2}$×100=50米，
則此時分割線的長度為50米．

（2）如圖3中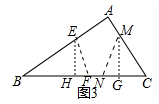，分割線分別為EF、MN，當BE=BF，CM=CN，S_△BEF=S_△CMN=800時，分割線之和最小．
作EH⊥BC于H，MG⊥BC于G．
∵∠B=∠B，∠EHB=∠A，
∴△BEH∽△BCA，
∴EH：BH：BE=3：4：5，設EH=3k，則BH=4k，BE=5k，HF=k，EF=$\sqrt{10}$k，
∵S_△BEF=$\frac{1}{2}$•3k•5k=800
∴k=$\frac{8\sqrt{15}}{3}$，
∴EF=$\frac{40\sqrt{6}}{3}$，
同理CG：GM：CM=3：4：5，設CG=3k，MG=4k，CM=5k，則GN=2k，MN=2$\sqrt{5}$k，
∵$\frac{1}{2}$×5k•4k=800，
∴k=4$\sqrt{5}$，
∴MN=40，
∴分割線之和為40+$\frac{40\sqrt{6}}{3}$．

點評 本題主要考查的是作圖--應用與設計作圖，此題主要考查三角形的面積等分問題；用到的知識點為：三角形的中線把三角形分成面積相等的兩部分，解題的關鍵是理解題意，第二個問題關鍵是分割成兩個等腰三角形時，分割線最短，屬于中考常考題型．