
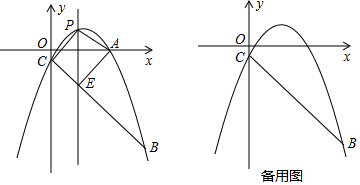
分析 (1)根據拋物線y=-$\frac{1}{3}$x2+bx+c經過點A(5,$\frac{2}{3}$)、點B(9,-10),運用待定系數法即可求得拋物線對應的函數表達式;
(2)根據直線BC為:y=-x-1,可設點P的坐標為(m,-$\frac{1}{3}$m2+2m-1),則E(m,-m-1),進而得到PE=-$\frac{1}{3}$m2+2m-1-(-m-1)=-$\frac{1}{3}$m2+3m,最后根據四邊形AECP的面積=△APE面積+△CPE面積,求得點P坐標為$(\frac{9}{2},\frac{5}{4})$;
(3)①根據∠PCB=90°,CF平分∠PCB,可得∠BCF=45°,進而得出CF∥x軸,則當y=-1時,-1=-$\frac{1}{3}$x2+2x-1,解得F(6,-1),再根據直線CP為:y=x-1,可得當x-1=-$\frac{1}{3}$x2+2x-1時,可得P(3,2);
②根據直線CB:y=-x-1,直線PF:-x+5,可得CB∥PF,即可得到∠BCF=∠PFC=45°,故在直線CF上存在滿足條件的點Q,再設Q(t,-1),由題可得CF=6,CB=9$\sqrt{2}$,PF=3$\sqrt{2}$,最后分兩種情況進行討論:當△PFQ1∽△BCF時,當△PFQ∽△FCB時,分別求得t的值,即可得出點Q的坐標為(4,-1)或(-3,-1).
解答 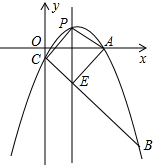 解:(1)∵拋物線y=-$\frac{1}{3}$x2+bx+c經過點A(5,$\frac{2}{3}$)、點B(9,-10),
解:(1)∵拋物線y=-$\frac{1}{3}$x2+bx+c經過點A(5,$\frac{2}{3}$)、點B(9,-10),
∴$\left\{\begin{array}{l}{\frac{2}{3}=-\frac{1}{3}×25+5b+c}\\{-10=-\frac{1}{3}×81+9b+c}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=2}\\{c=-1}\end{array}\right.$,
∴拋物線對應的函數表達式為y=-$\frac{1}{3}$x2+2x-1;
(2)由拋物線可得,C(0,-1),B(9,-10),
∴直線BC為:y=-x-1,
設點P的坐標為(m,-$\frac{1}{3}$m2+2m-1),則E(m,-m-1),
∴PE=-$\frac{1}{3}$m2+2m-1-(-m-1)=-$\frac{1}{3}$m2+3m,
∴四邊形AECP的面積=△APE面積+△CPE面積
=$\frac{1}{2}$×(-$\frac{1}{3}$m2+3m)×m+$\frac{1}{2}$×(-$\frac{1}{3}$m2+3m)×(5-m)
=$\frac{5}{2}$(-$\frac{1}{3}$m2+3m)
=-$\frac{5}{6}$m2+$\frac{15}{2}$m,
=-$\frac{5}{6}$(m-$\frac{9}{2}$)2+$\frac{135}{8}$,
∴當m=$\frac{9}{2}$時,-$\frac{1}{3}$m2+2m-1=$\frac{5}{4}$,
∴點P坐標為$(\frac{9}{2},\frac{5}{4})$;
(3)①過點B作BH⊥y軸于H,
∵C(0,-1),B(9,-10),
∴CH=BH=9,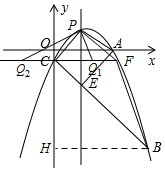
∴∠BCH=45°,
∵∠PCB=90°,CF平分∠PCB,
∴∠BCF=45°,
∴∠FCH=90°,即CF∥x軸,
當y=-1時,-1=-$\frac{1}{3}$x2+2x-1,
解得x1=0,x2=6,
∴F(6,-1),
∵CP⊥CB,C(0,-1),
∴直線CP為:y=x-1,
當x-1=-$\frac{1}{3}$x2+2x-1時,解得x1=0,x2=3,
當x=3時,y=2,
∴P(3,2);
②∵直線CB:y=-x-1,直線PF:y=-x+5,
∴CB∥PF,
∴∠BCF=∠PFC=45°,
∴在直線CF上存在滿足條件的點Q,
設Q(t,-1),
由題可得CF=6,CB=9$\sqrt{2}$,PF=3$\sqrt{2}$,
(ⅰ)如圖所示,當△PFQ1∽△BCF時,
$\frac{CF}{F{Q}_{1}}$=$\frac{BC}{PF}$,即$\frac{6}{6-t}$=$\frac{9\sqrt{2}}{3\sqrt{2}}$,
解得t=4,
∴Q1(4,-1);
(ⅱ)如圖所示,當△PFQ∽△FCB時,
$\frac{CF}{FP}$=$\frac{BC}{{Q}_{2}F}$,即$\frac{6}{3\sqrt{2}}$=$\frac{9\sqrt{2}}{6-t}$,
解得t=-3,
∴Q2(-3,-1).
綜上所述,點Q的坐標為(4,-1)或(-3,-1).
點評 本題屬于二次函數綜合題,主要考查了二次函數的綜合應用,相似三角形的判定與性質以及解一元二次方程的方法,解第(2)問時需要運用配方法,解第(3)問時需要運用分類討論思想.


科目:初中數學 來源: 題型:選擇題
| A. | 13 | B. | 14 | C. | 17 | D. | 13或14 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,邊長為2的菱形ABCD中,∠BAD=60°,現有∠BFE=30°的三角板△BEF,將△BEF繞B旋轉得△BE′F′,BE′,BF′所在直線分別交線段AC于點M,N,若點C關于直線BE′的對稱點為C′,當C′N⊥AC時,AN的長為$\sqrt{3}$-1.
如圖,邊長為2的菱形ABCD中,∠BAD=60°,現有∠BFE=30°的三角板△BEF,將△BEF繞B旋轉得△BE′F′,BE′,BF′所在直線分別交線段AC于點M,N,若點C關于直線BE′的對稱點為C′,當C′N⊥AC時,AN的長為$\sqrt{3}$-1.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
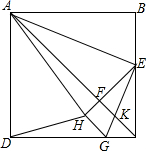 如圖所示,在邊長為10的正方形ABCD中,AC是對角線,點E,G分別是邊BC,CD上的點,將△ABE沿AE折疊得到△AFE,且F恰好落在對角線AC上,同理將△CEG沿GE折疊得到△HEG,使得EH與EF重合,連接AH,DH.
如圖所示,在邊長為10的正方形ABCD中,AC是對角線,點E,G分別是邊BC,CD上的點,將△ABE沿AE折疊得到△AFE,且F恰好落在對角線AC上,同理將△CEG沿GE折疊得到△HEG,使得EH與EF重合,連接AH,DH.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2.916×106米 | B. | 2.916×105米 | C. | 29.16×105米 | D. | 2.916×104米 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com