
分析 (1)令y=0求得x即可得;
(2)根據(jù)△ABP的面積為10求得P點(diǎn)縱坐標(biāo)的絕對值,再由y=5或y=-5分別求出x即可得.
解答 解:(1)令y=0得:x2-2x-3=0,
解得:x=-1或x=3,
∴點(diǎn)A(-1,0)、B(3,0);
(2)∵AB=4,且S△ABP=10,
∴$\frac{1}{2}$AB•|yP|=10,即$\frac{1}{2}$×4•|yP|=10,
解得:|yP|=5,
當(dāng)y=5時,由x2-2x-3=5,得:x=-2或x=4,
即點(diǎn)P坐標(biāo)為(-2,5)或(4,5),
當(dāng)y=-5時,x2-2x-3=-5,方程無解;
綜上,P點(diǎn)坐標(biāo)為(-2,5)或(4,5).
點(diǎn)評 本題主要考查拋物線與x軸的交點(diǎn),根據(jù)三角形的面積求得點(diǎn)P的縱坐標(biāo)是解題的關(guān)鍵.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{1-{a}^{2}}{-a}$=$\frac{{a}^{2}-1}{a}$ | B. | $\frac{-1-{a}^{2}}{-a}$=$\frac{1-{a}^{2}}{a}$ | ||
| C. | $\frac{-ab}{a-b}$=$\frac{ab}{b-a}$ | D. | $\frac{(a-b)^{2}}{{a}^{2}-{b}^{2}}$=$\frac{a-b}{a+b}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
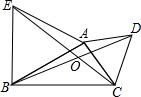 如圖,分別以△ABC的邊AB、AC向外作等邊△ABE和等邊△ACD,直線BD與直線CE相交于點(diǎn)O.
如圖,分別以△ABC的邊AB、AC向外作等邊△ABE和等邊△ACD,直線BD與直線CE相交于點(diǎn)O.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
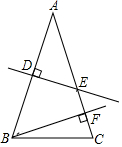 如圖,△ABC中,AB=AC,AB的垂直平分線交AB于D,交AC于E,EC的垂直平分線恰好經(jīng)過點(diǎn)B.求∠A的度數(shù).
如圖,△ABC中,AB=AC,AB的垂直平分線交AB于D,交AC于E,EC的垂直平分線恰好經(jīng)過點(diǎn)B.求∠A的度數(shù).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com