
 如圖,在半徑為4,圓心角為90°的扇形內,以BC為直徑作半圓交AB于點D,連接CD,則陰影部分的面積是4π-4.(結果保留π)
如圖,在半徑為4,圓心角為90°的扇形內,以BC為直徑作半圓交AB于點D,連接CD,則陰影部分的面積是4π-4.(結果保留π) 分析 根據BC為直徑可知∠CDB=90°,在等腰直角三角形ABC中,CD垂直平分AB,CD=DB,D為半圓的中點,陰影部分的面積可以看作是扇形ACB的面積與△ADC的面積之差.
解答 解:在Rt△ACB中,
∵AC=BC=4,
∴AB=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
∵BC是半圓的直徑,
∴∠CDB=90°,
在等腰Rt△ACB中,
∵CD垂直平分AB,CD=BD=2$\sqrt{2}$,
∴D為半圓的中點,
S陰影部分=S扇形ACB-S△ADC=$\frac{1}{4}$π×42-$\frac{1}{2}$×(2$\sqrt{2}$)2=4π-4.
故答案為:4π-4.
點評 本題考查的是扇形面積的計算,熟記扇形的面積公式是解答此題的關鍵.


 學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目:初中數學 來源: 題型:選擇題
 如圖,在平面直角坐標系中,點P坐標為(-4,3),以點B(-1,0)為圓心,以BP的長為半徑畫弧,交x軸的負半軸于點A,則點A的橫坐標介于( )
如圖,在平面直角坐標系中,點P坐標為(-4,3),以點B(-1,0)為圓心,以BP的長為半徑畫弧,交x軸的負半軸于點A,則點A的橫坐標介于( )| A. | -6和-5之間 | B. | -5和-4之間 | C. | -4和-3之間 | D. | -3和-2之間 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2.03kg | B. | 2.02kg | C. | 2.0kg | D. | 2kg |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
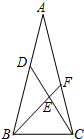 如圖,在△ABC中,AB=AC,點D在邊AB上,點E在線段CD上,且∠BEC=∠ACB,BE的延長線與邊AC相交于點F,則與∠BDC相等的角是( )
如圖,在△ABC中,AB=AC,點D在邊AB上,點E在線段CD上,且∠BEC=∠ACB,BE的延長線與邊AC相交于點F,則與∠BDC相等的角是( )| A. | ∠DBE | B. | ∠CBE | C. | ∠BCE | D. | ∠A |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,CD是⊙O的直徑,且CD=4cm,點P為CD的延長線上一點,過點P作⊙O的切線PA、PB,切點分別為A、B.
如圖,CD是⊙O的直徑,且CD=4cm,點P為CD的延長線上一點,過點P作⊙O的切線PA、PB,切點分別為A、B.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com