
 如圖,AB是⊙O的一條弦,C,D是⊙O上的兩個動點(diǎn),且在AB弦的異側(cè),連接CD.
如圖,AB是⊙O的一條弦,C,D是⊙O上的兩個動點(diǎn),且在AB弦的異側(cè),連接CD.分析 (1)證$\widehat{AC}=\widehat{BC}$=$\widehat{AD}$,即可得$\widehat{DAC}=\widehat{ACB}$,從而得證;
(2)由S四邊形ABCD=S△ADB+S△ACB,設(shè)△ADB和△ACB的公共邊AB上的高為h1、h2,則h1+h2的最大值為⊙O的直徑,即當(dāng)點(diǎn)C在劣弧AB的中點(diǎn)、點(diǎn)D在優(yōu)弧AB的中點(diǎn)時,四邊形ABCD的面積最大,根據(jù)∠ADB=45°知∠AOB=90°,根據(jù)AO=BO=1得AB=$\sqrt{2}$,由S四邊形ABCD=$\frac{1}{2}$AB(h1+h2)可得答案.
解答 解:(1)∵AC=BC,
∴$\widehat{AC}=\widehat{BC}$,
∵AB平分∠CBD,
∴∠CBA=∠DBA,
∴$\widehat{AC}=\widehat{AD}$,
∴$\widehat{DAC}=\widehat{ACB}$,
∴AB=CD;
(2)∵S四邊形ABCD=S△ADB+S△ACB,
設(shè)△ADB和△ACB的公共邊AB上的高為h1、h2,則h1+h2的最大值為⊙O的直徑,
即當(dāng)點(diǎn)C在劣弧AB的中點(diǎn)、點(diǎn)D在優(yōu)弧AB的中點(diǎn)時,四邊形ABCD的面積最大,
如圖,連接OA、OB,
∵∠ADB=45°,
∴∠AOB=90°,
∵AO=BO=1,
∴AB=$\sqrt{2}$,
∴S四邊形ABCD=$\frac{1}{2}$AB(h1+h2)=$\frac{1}{2}$×$\sqrt{2}$×2=$\sqrt{2}$.
點(diǎn)評 本題主要考查圓周角定理、角平分線的性質(zhì)、勾股定理等知識點(diǎn),由△ADB和△ACB的公共邊AB上的高為h1、h2,則h1+h2的最大值為⊙O的直徑時,四邊形ABCD的面積最大是解題的關(guān)鍵.


 狀元及第系列答案
狀元及第系列答案 同步奧數(shù)系列答案
同步奧數(shù)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
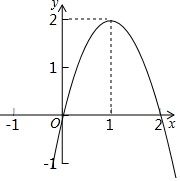 二次函數(shù)y=ax2+bx+c(a≠0)的圖象如圖所示,根據(jù)圖象回答下列問題.
二次函數(shù)y=ax2+bx+c(a≠0)的圖象如圖所示,根據(jù)圖象回答下列問題.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
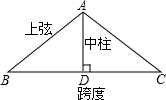 如圖,廠房屋頂人字架(等腰三角形)的跨度為20m,∠B=37°,求中柱AD(D為底邊中點(diǎn))和上弦AB的長(參考數(shù)據(jù):cos37°≈0.6)
如圖,廠房屋頂人字架(等腰三角形)的跨度為20m,∠B=37°,求中柱AD(D為底邊中點(diǎn))和上弦AB的長(參考數(shù)據(jù):cos37°≈0.6)查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
| 甲 | 80 | 75 | 90 | 64 | 88 | 95 |
| 乙 | 84 | 80 | 88 | 76 | 79 | 85 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
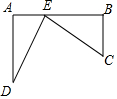 如圖,鐵路上A,B兩站(視為線上兩點(diǎn))相距25千米,C,D為鐵路同旁兩個村莊(視為兩點(diǎn)),DA⊥AB于A點(diǎn),CB⊥AB于B點(diǎn),DA=15千米,CB=10千米,現(xiàn)在要在鐵路AB上修一個土特品回購站E,使C,D兩村莊到E站的距離相等,則E站應(yīng)建在距A站10千米處.
如圖,鐵路上A,B兩站(視為線上兩點(diǎn))相距25千米,C,D為鐵路同旁兩個村莊(視為兩點(diǎn)),DA⊥AB于A點(diǎn),CB⊥AB于B點(diǎn),DA=15千米,CB=10千米,現(xiàn)在要在鐵路AB上修一個土特品回購站E,使C,D兩村莊到E站的距離相等,則E站應(yīng)建在距A站10千米處.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com