
分析 將原式根據分式的混合運算順序和法則化簡后,把a、b的值代入計算可得.
解答 解:原式=$\frac{a-b}{a}$÷$\frac{{a}^{2}-2ab+{b}^{2}}{a}$
=$\frac{a-b}{a}$•$\frac{a}{(a-b)^{2}}$
=$\frac{1}{a-b}$,
當a=$\frac{\sqrt{3}}{2}$$+\frac{1}{5}$,b=$\frac{\sqrt{3}}{2}$$-\frac{1}{5}$時,
原式=$\frac{1}{\frac{\sqrt{3}}{2}+\frac{1}{5}-(\frac{\sqrt{3}}{2}-\frac{1}{5})}$=$\frac{5}{2}$.
點評 本題主要考查分式的化簡求值,熟練掌握分式的混合運算順序和法則是解題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:填空題
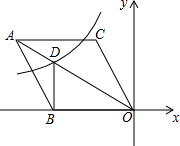 如圖,在平面直角坐標系中,菱形ABOC的頂點O在坐標原點,邊BO在x軸的負半軸上,頂點C的坐標為(-3,3$\sqrt{3}}$),反比例函數y=$\frac{k}{x}$的圖象與菱形對角線AO交于D點,連接BD,當BD⊥x軸時,k的值是-12$\sqrt{3}$.
如圖,在平面直角坐標系中,菱形ABOC的頂點O在坐標原點,邊BO在x軸的負半軸上,頂點C的坐標為(-3,3$\sqrt{3}}$),反比例函數y=$\frac{k}{x}$的圖象與菱形對角線AO交于D點,連接BD,當BD⊥x軸時,k的值是-12$\sqrt{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
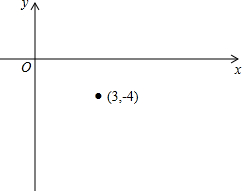 已知反比例函數y=$\frac{k}{x}$的圖象經過點(-3,4).
已知反比例函數y=$\frac{k}{x}$的圖象經過點(-3,4).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com