
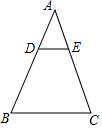
 如圖,在△ABC中,已知點D在AB上,DB=2AD,DE∥BC交AC于E,則下列結論正確的有( )
如圖,在△ABC中,已知點D在AB上,DB=2AD,DE∥BC交AC于E,則下列結論正確的有( )| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
分析 由DE∥BC可得到△ADE∽△ABC則可對③進行判斷;根據相似三角形的性質得$\frac{DE}{BC}$=$\frac{AE}{AC}$=$\frac{AD}{AB}$=$\frac{1}{3}$,則可對①②進行判斷;然后根據比例的性質可對④進行判斷.
解答 解:∵DE∥BC,
∴△ADE∽△ABC,所以③正確;
∴$\frac{DE}{BC}$=$\frac{AE}{AC}$=$\frac{AD}{AB}$,
而DB=2AD,
即AB=3AD,
∴$\frac{DE}{BC}$=$\frac{AE}{AC}$=$\frac{1}{3}$,
∴BC=3DE,AE=$\frac{1}{3}$AC,所以①錯誤,②正確;
∴$\frac{BD}{BA}$=$\frac{CE}{CA}$=$\frac{1}{3}$,所以④正確.
故選C.
點評 本題考查了相似三角形的判定與性質:在判定兩個三角形相似時,應注意利用圖形中已有的公共角、公共邊等隱含條件,以充分發揮基本圖形的作用,尋找相似三角形的一般方法是通過作平行線構造相似三角形.在應用相似三角形的性質時,主要利用相似三角形的性質進行幾何計算.


科目:初中數學 來源: 題型:選擇題
| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖是用相同的正方形磚鋪成的地面,一寶物藏在其中某一塊磚的下面,則寶物在白色區域的概率是( )
如圖是用相同的正方形磚鋪成的地面,一寶物藏在其中某一塊磚的下面,則寶物在白色區域的概率是( )| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{7}{15}$ | D. | $\frac{8}{15}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com