
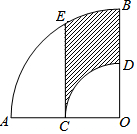
 如圖,在扇形AOB中,∠AOB=90°,點C為OA的中點,CE⊥OA交弧AB于點E,以點O為圓心,OC的長為半徑作弧CD交OB于點D,若OA=2,則陰影部分的面積為( )
如圖,在扇形AOB中,∠AOB=90°,點C為OA的中點,CE⊥OA交弧AB于點E,以點O為圓心,OC的長為半徑作弧CD交OB于點D,若OA=2,則陰影部分的面積為( )| A. | $\frac{4π-3\sqrt{3}}{4}$ | B. | $\frac{π-\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{2}$+$\frac{π}{12}$ | D. | $\frac{π-3\sqrt{3}}{2}$ |
分析 連接OE、AE,根據點C為OC的中點可得∠CEO=30°,繼而可得△AEO為等邊三角形,求出扇形AOE的面積,最后用扇形AOB的面積減去扇形COD的面積,再減去S空白AEC即可求出陰影部分的面積.
解答 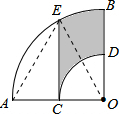 解:連接OE、AE,
解:連接OE、AE,
∵點C為OA的中點,
∴∠CEO=30°,∠EOC=60°,
∴△AEO為等邊三角形,
∴S扇形AOE=$\frac{60π×{2}^{2}}{360}$=$\frac{2}{3}$π,
∴S陰影=S扇形AOB-S扇形COD-(S扇形AOE-S△COE)
=$\frac{90π×{2}^{2}}{360}$-$\frac{90π×{2}^{2}}{360}$-($\frac{2}{3}$π-$\frac{1}{2}$×1×$\sqrt{3}$)
=$\frac{3}{4}$π-$\frac{2}{3}$π+$\frac{\sqrt{3}}{2}$
=$\frac{π}{12}$+$\frac{\sqrt{3}}{2}$.
故選C.
點評 本題考查了扇形的面積計算,解答本題的關鍵是掌握扇形的面積公式:S=$\frac{nπ{r}^{2}}{360}$.


 智慧小復習系列答案
智慧小復習系列答案科目:初中數學 來源: 題型:選擇題
| A. | 100 | B. | 200 | C. | 300 | D. | 400 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| a | 0.000001 | 0.001 | 1 | 1000 | 1000000 |
| $\root{3}{a}$ | 0.01 | 0.1 | 1 | 10 | 100 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,菱形ABCD的邊長為5,對角線AC=8.
如圖,菱形ABCD的邊長為5,對角線AC=8.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
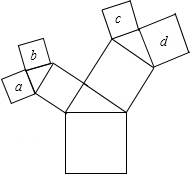 在如圖所示的圖形中,所有的四邊形都是正方形,所有的三角形都是直角三角形,若最大正方形的邊長為7cm,則正方形a,b,c,d的面積之和是147cm2.
在如圖所示的圖形中,所有的四邊形都是正方形,所有的三角形都是直角三角形,若最大正方形的邊長為7cm,則正方形a,b,c,d的面積之和是147cm2.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com