
分析 (1)將(7,16)、(5,0)代入y=ax2+bx-75,解方程組即可得;
(2)配方成頂點式即可得最值情況;
(3)根據函數值大于或等于16,可得不等式的解集,可得答案.
解答 解:(1)將點(7,16)、(5,0)代入y=ax2+bx-75,
得:$\left\{\begin{array}{l}{49a+7b-75=16}\\{25a+5b-75=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=20}\end{array}\right.$,
故拋物線解析式為:y=-x2+20x-75
(2)y=-x2+20x-75=-(x-10)2+25,
當x=10是,y取得最大值25,
答:銷售單價為10元時,該種商品每天的銷售利潤最大,最大利潤為25元;
(2)∵函數y=-x2+20x-75圖象的對稱軸為直線x=10,
可知點(7,16)關于對稱軸的對稱點是(13,16),
又∵函數y=-x2+20x-75圖象開口向下,
∴當7≤x≤13時,y≥16.
答:銷售單價不少于7元且不超過13元時,該種商品每天的銷售利潤不低于16元.
點評 本題考查了待定系數求二次函數解析式、二次函數的圖象與性質,熟練掌握二次函數的圖象與性質是關鍵.


科目:初中數學 來源: 題型:填空題
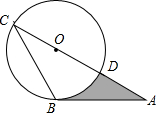 如圖,AB是⊙O的切線,B為切點,AC經過點O,與⊙O分別相交于點D,C,若∠ACB=30°,AB=$\sqrt{3}$,則陰影部分的面積是$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
如圖,AB是⊙O的切線,B為切點,AC經過點O,與⊙O分別相交于點D,C,若∠ACB=30°,AB=$\sqrt{3}$,則陰影部分的面積是$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在扇形ACB中,∠ACB=90°,BC為直徑作半圓,圓心為O.過點O作AC的平行線交兩弧于點D、E,若BC=2,則陰影部分的面積是$\frac{5}{12}$π-$\frac{\sqrt{3}}{2}$.
如圖,在扇形ACB中,∠ACB=90°,BC為直徑作半圓,圓心為O.過點O作AC的平行線交兩弧于點D、E,若BC=2,則陰影部分的面積是$\frac{5}{12}$π-$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (-$\frac{1}{2}$)-2 | B. | -(-$\frac{1}{2}$)0 | C. | (-$\frac{1}{2}$)3 | D. | -|$\frac{1}{2}$| |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
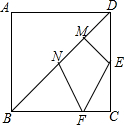 正方形ABCD,AB=4,E是CD中點,BF=3CF,點M,N為線段BD上的動點,MN=$\sqrt{2}$,求四邊形EMNF周長的最小值$\sqrt{13}$+$\sqrt{2}$+$\sqrt{5}$.
正方形ABCD,AB=4,E是CD中點,BF=3CF,點M,N為線段BD上的動點,MN=$\sqrt{2}$,求四邊形EMNF周長的最小值$\sqrt{13}$+$\sqrt{2}$+$\sqrt{5}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
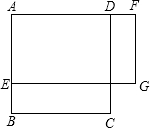 如圖,正方形ABCD的邊長為5,點E是AB上一點,點F是AD延長線上一點,且BE=DF.四邊形AEGF是矩形,則矩形AEGF的面積y與BE的長x之間的函數關系式為( )
如圖,正方形ABCD的邊長為5,點E是AB上一點,點F是AD延長線上一點,且BE=DF.四邊形AEGF是矩形,則矩形AEGF的面積y與BE的長x之間的函數關系式為( )| A. | y=5-x | B. | y=5-x2 | C. | y=25-x | D. | y=25-x2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com