
 如圖,在扇形ACB中,∠ACB=90°,BC為直徑作半圓,圓心為O.過點O作AC的平行線交兩弧于點D、E,若BC=2,則陰影部分的面積是$\frac{5}{12}$π-$\frac{\sqrt{3}}{2}$.
如圖,在扇形ACB中,∠ACB=90°,BC為直徑作半圓,圓心為O.過點O作AC的平行線交兩弧于點D、E,若BC=2,則陰影部分的面積是$\frac{5}{12}$π-$\frac{\sqrt{3}}{2}$. 分析 如圖,連接CE.圖中S陰影=S扇形BCE-S扇形BOD-S△OCE.根據已知條件易求得OB=OC=OD=1,BC=CE=2.∠ECB=60°,OE=$\sqrt{3}$,所以由扇形面積公式、三角形面積公式進行解答即可.
解答 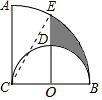 解:如圖,連接CE.
解:如圖,連接CE.
∵AC⊥BC,AC=BC=2,以BC為直徑作半圓,圓心為點O;以點C為圓心,BC為半徑作弧AB,
∴∠ACB=90°,OB=OC=OD=1,BC=CE=2.
又∵OE∥AC,
∴∠ACB=∠COE=90°.
∴在直角△OEC中,OC=1,CE=2,
∴∠CEO=30°,∠ECB=60°,OE=$\sqrt{3}$,
∴S陰影=S扇形BCE-S扇形BOD-S△OCE=$\frac{60π•{2}^{2}}{360}$-$\frac{1}{4}$π×12-$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{2}{3}$π-$\frac{1}{4}$π-$\frac{\sqrt{3}}{2}$=$\frac{5}{12}$π-$\frac{\sqrt{3}}{2}$,
故答案為:$\frac{5}{12}$π-$\frac{\sqrt{3}}{2}$.
點評 本題考查了扇形面積的計算.不規則圖形的面積一定要注意分割成規則圖形的面積進行計算.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 373.9×108元 | B. | 37.39×109元 | C. | 3.739×1010元 | D. | 0.3739×1011 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
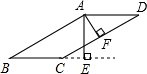 如圖,在平行四邊形ABCD中,AE⊥BC,AF⊥CD,點E,F為垂足,∠EAF=30°,AE=3cm,AF=2cm,求平行四邊形ABCD的周長.
如圖,在平行四邊形ABCD中,AE⊥BC,AF⊥CD,點E,F為垂足,∠EAF=30°,AE=3cm,AF=2cm,求平行四邊形ABCD的周長.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com