
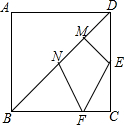
 正方形ABCD,AB=4,E是CD中點,BF=3CF,點M,N為線段BD上的動點,MN=$\sqrt{2}$,求四邊形EMNF周長的最小值$\sqrt{13}$+$\sqrt{2}$+$\sqrt{5}$.
正方形ABCD,AB=4,E是CD中點,BF=3CF,點M,N為線段BD上的動點,MN=$\sqrt{2}$,求四邊形EMNF周長的最小值$\sqrt{13}$+$\sqrt{2}$+$\sqrt{5}$. 分析 先作點E關于BD的對稱點G,則點G在AD上,連接GM,過G作BD的平行線,截取GH=MN=$\sqrt{2}$,連接HN,則四邊形GHNM是平行四邊形,進而得出HN=GM=EM,
過H作PQ⊥BC,交AD于P,交BC于Q,則∠HPG=∠HQF=90°,PQ=AB=4,當點H、N、F在同一直線上時,HN+NF=HF(最短),此時ME+NF最短,最后根據勾股定理求得HF和EF的長,即可得到四邊形EMNF周長的最小值.
解答  解:作點E關于BD的對稱點G,則點G在AD上,
解:作點E關于BD的對稱點G,則點G在AD上,
連接GM,過G作BD的平行線,截取GH=MN=$\sqrt{2}$,連接HN,則四邊形GHNM是平行四邊形,
∴HN=GM=EM,
過H作PQ⊥BC,交AD于P,交BC于Q,則∠HPG=∠HQF=90°,PQ=AB=4,
∵∠PGH=∠ADB=45°,
∴HP=PG=$\frac{HG}{\sqrt{2}}$=1,HQ=4-1=3,
由軸對稱的性質,可得DG=ED=2,
∴AP=4-2-1=1,
∴BQ=1,
又∵BF=3CF,BC=4,
∴CF=1,
∴QF=4-1-1=2,
∵當點H、N、F在同一直線上時,HN+NF=HF(最短),
此時ME+NF最短,
∴Rt△HQF中,FH=$\sqrt{H{Q}^{2}+F{Q}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
即ME+NF最短為$\sqrt{13}$,
又∵Rt△CEF中,EF=$\sqrt{C{E}^{2}+C{F}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∴ME+NF+MN+EF=$\sqrt{13}$+$\sqrt{2}$+$\sqrt{5}$,
∴四邊形EMNF周長的最小值為$\sqrt{13}$+$\sqrt{2}$+$\sqrt{5}$.
故答案為:$\sqrt{13}$+$\sqrt{2}$+$\sqrt{5}$.
點評 本題主要考查了最短路線問題,正方形的性質,勾股定理,軸對稱的性質以及平行四邊形的性質的綜合應用,解決問題的關鍵是作輔助線構造平行四邊形和直角三角形,依據兩點之間,線段最短進行求解.凡是涉及最短距離的問題,一般要考慮線段的性質定理,多數情況要作點關于某直線的對稱點.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
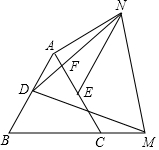 如圖,等邊△ABC中,AB=8,點D、E分別為AB、AC的中點,點M為射線BC上一動點,以DM為一邊作等邊△DMN.∠DAN=150°,DN交AE于F,線段NF的長為$\frac{2\sqrt{7}}{3}$.
如圖,等邊△ABC中,AB=8,點D、E分別為AB、AC的中點,點M為射線BC上一動點,以DM為一邊作等邊△DMN.∠DAN=150°,DN交AE于F,線段NF的長為$\frac{2\sqrt{7}}{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com