
分析 設(shè)等腰直角三角形的直角邊長為x,利用直角邊與斜邊之間的比例即可求出x的值,然后利用面積公式即可求出答案.
解答 解:設(shè)等腰直角三角形的直角邊長為x,
∴斜邊長為:$\sqrt{2}$x,
∴$\sqrt{2}$x+2x=2a,
∴x=(2-$\sqrt{2}$)a
∴斜邊長為:$\sqrt{2}$x=(2$\sqrt{2}$-2)a
∴面積為:$\frac{1}{2}$x2=(3-2$\sqrt{2}$)a2
故答案為:(2$\sqrt{2}$-2)a;(3-2$\sqrt{2}$)a2
點評 本題考查等腰直角三角形的性質(zhì),解題的關(guān)鍵是設(shè)直角邊為x,然后列出方程求出x的值,本題屬于基礎(chǔ)題型.


 各地期末復(fù)習(xí)特訓(xùn)卷系列答案
各地期末復(fù)習(xí)特訓(xùn)卷系列答案 小博士期末闖關(guān)100分系列答案
小博士期末闖關(guān)100分系列答案科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
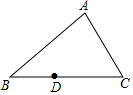 如圖,點D在BC邊上,過D點作DE∥BA交AC于點E,作DF∥CA交AB于點F,請你補全圖形,判斷∠EDF與∠A的數(shù)量關(guān)系,并證明你的結(jié)論.
如圖,點D在BC邊上,過D點作DE∥BA交AC于點E,作DF∥CA交AB于點F,請你補全圖形,判斷∠EDF與∠A的數(shù)量關(guān)系,并證明你的結(jié)論.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
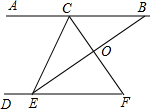 如圖,點C、E分別在直線AB、DF上,小華想知道∠ACE和∠DEC是否互補,但是他沒有帶量角器,只帶了一副三角板,于是他想了這樣一個辦法:首先連結(jié)DF,再找出CF的中點O,然后連結(jié)EO并延長EO和直線AB相交于點B,經(jīng)過測量,他發(fā)現(xiàn)EO=BO,因此他得出結(jié)論:∠ACE和∠DEC互補,而且他還發(fā)現(xiàn)BC=EF.小華的想法對嗎?為什么?
如圖,點C、E分別在直線AB、DF上,小華想知道∠ACE和∠DEC是否互補,但是他沒有帶量角器,只帶了一副三角板,于是他想了這樣一個辦法:首先連結(jié)DF,再找出CF的中點O,然后連結(jié)EO并延長EO和直線AB相交于點B,經(jīng)過測量,他發(fā)現(xiàn)EO=BO,因此他得出結(jié)論:∠ACE和∠DEC互補,而且他還發(fā)現(xiàn)BC=EF.小華的想法對嗎?為什么?查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com