
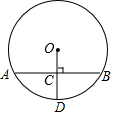
 如圖,已知半徑OD與弦AB互相垂直,垂足為點C,若AB=8,CD=3,則⊙O的半徑為( )
如圖,已知半徑OD與弦AB互相垂直,垂足為點C,若AB=8,CD=3,則⊙O的半徑為( )| A. | $\frac{19}{6}$ | B. | 4 | C. | 5 | D. | $\frac{25}{6}$ |
分析 連接半徑,根據(jù)垂徑定理,構(gòu)建直角三角形,并求BC的長為4,設(shè)半徑為r,根據(jù)勾股定理列方程可求出結(jié)論.
解答  解:連接OB,
解:連接OB,
設(shè)⊙O的半徑為r,則OD=OB=r,OC=r-3,
∵AB⊥OD,
∴BC=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4,∠OCB=90°,
由勾股定理得:OB2=OC2+BC2,
r2=(r-3)2+42,
解得:r=$\frac{25}{6}$,
則⊙O的半徑為$\frac{25}{6}$,
故選D.
點評 本題主要考查了垂徑定理、勾股定理,熟練掌握垂徑定理是關(guān)鍵,比較簡單,是常考題型.


科目:初中數(shù)學(xué) 來源: 題型:解答題
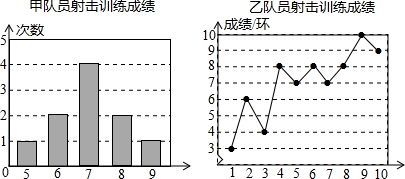
| 平均成績/環(huán) | 中位數(shù)/環(huán) | 眾數(shù)/環(huán) | 方差 | |
| 甲 | 7 | b | 7 | c |
| 乙 | a | 7.5 | 8 | 4.2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
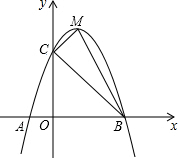 如圖,拋物線y=ax2+bx+c交x軸于A(-1,0)、B兩點,交y軸于點C(0,5),且過點D(1,8),M為其頂點.
如圖,拋物線y=ax2+bx+c交x軸于A(-1,0)、B兩點,交y軸于點C(0,5),且過點D(1,8),M為其頂點.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,AB是⊙O的直徑,弦CD⊥AB于點M,連結(jié)CO,CB.
如圖,AB是⊙O的直徑,弦CD⊥AB于點M,連結(jié)CO,CB.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com