
 如圖,已知?ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.
如圖,已知?ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.分析 (1)AE平分∠BAD,則∠BAE=∠DAE;AB∥CD,則∠BAE=∠DEA,從而有∠DAE=∠DEA,所以,DE=DA,由勾股定理求出DF,得出AD,即可求出DE的長;
(2)結(jié)論:AB=DG+FC;將△CDF平移到△ABH的位置,將△ADG順時針旋轉(zhuǎn)90°到△AHI的位置,證明∠I=∠AGD=∠GAH=∠BAI,進(jìn)一步得出結(jié)論.
解答 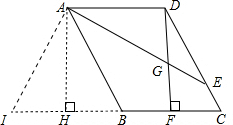 (1)解:∵四邊形ABCD是平行四邊形,
(1)解:∵四邊形ABCD是平行四邊形,
∴AD=BC,AB∥DC.CD=AB=5,
∴∠BAE=∠DEA.
∵AE平分∠BAD,
∴∠BAE=∠DAE.
∴∠DEA=∠DAE.
∴AD=DE.
∵DF⊥BC,
∴DF=$\sqrt{C{D}^{2}-C{F}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴AD=DF=4,
∴DE=4;
(2)證明:∵四邊形ABCD是平行四邊形,
∴AB=DC,AD=BC,AB∥DC,AD∥BC,
∴∠ABC+∠C=180°,
把△DFC沿射線DA方向平移,平移距離為AD,則DC與AB重合,記平移后的三角形為△ABH,如圖所示:
則∠AHB=∠DFC=90°,∠ABH=∠C,AH=DF,HB=FC
∵∠ABH+∠ABC=∠C+∠ABC=180°,
∴F,B,H三點(diǎn)共線,
∴BF+HB=BF+FC,從而FH=BC=AD=DF=AH.
∴四邊形AHFD為正方形.
∴∠ADF=90°,AH∥DF.
把△ADG繞點(diǎn)A順時針旋轉(zhuǎn)90°,則AD與AH重合,
∠DAG=∠HAI,∠DGA=∠HIA,∠AHI=∠ADG=90°,
∴∠AHB+∠AHI=∠AHB+∠ADG=180°,
∴I,H,B三點(diǎn)共線.
∵AE平分∠BAD,
∴∠BAG=∠DAG,
∴∠HAB+∠BAG=∠HAB+∠DAG=∠HAB+∠HAI.
即∠HAG=∠IAB.
∵AH∥DF,
∴∠HAG=∠DGA,
∴∠BIA=∠DGA=∠BAI.
∴AB=IB.
∵IB=IH+HB=DG+FC,
∴AB=CF+DG.
點(diǎn)評 本題考查了平行四邊形的性質(zhì),等腰三角形的判斷,用平移,旋轉(zhuǎn)的方法證明問題的能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
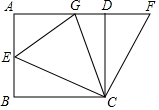 如圖1,在邊長4的正方形ABCD中,E是AB邊上一動點(diǎn)(不與A、B重合),F(xiàn)是AD延長線上一點(diǎn),且滿足DF=BE,以CE為邊作∠ECG=45°,交AD于點(diǎn)G.
如圖1,在邊長4的正方形ABCD中,E是AB邊上一動點(diǎn)(不與A、B重合),F(xiàn)是AD延長線上一點(diǎn),且滿足DF=BE,以CE為邊作∠ECG=45°,交AD于點(diǎn)G.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 在△ABC中,AD為角BAC平分線,DE⊥AB于E,DF⊥AC于F,AB=10厘米,AC=8厘米,△ABC的面積為45平分厘米,求DE的長.
在△ABC中,AD為角BAC平分線,DE⊥AB于E,DF⊥AC于F,AB=10厘米,AC=8厘米,△ABC的面積為45平分厘米,求DE的長.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
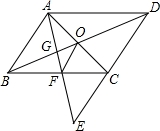 如圖,E為?ABCD中DC邊的延長線上一點(diǎn),且CE=DC.判斷AB與OF的位置關(guān)系和數(shù)量關(guān)系,并說明理由.
如圖,E為?ABCD中DC邊的延長線上一點(diǎn),且CE=DC.判斷AB與OF的位置關(guān)系和數(shù)量關(guān)系,并說明理由.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
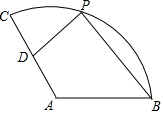 如圖,在扇形CAB中,CA=4,∠CAB=120°,D為CA的中點(diǎn),P為$\widehat{BC}$上一動點(diǎn)(不與C,B重合),則2PD+PB的最小值為( )
如圖,在扇形CAB中,CA=4,∠CAB=120°,D為CA的中點(diǎn),P為$\widehat{BC}$上一動點(diǎn)(不與C,B重合),則2PD+PB的最小值為( )| A. | 4+2$\sqrt{3}$ | B. | 4$\sqrt{7}$ | C. | 10 | D. | 4$\sqrt{3}$+4 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com