
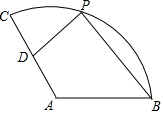
 如圖,在扇形CAB中,CA=4,∠CAB=120°,D為CA的中點,P為$\widehat{BC}$上一動點(不與C,B重合),則2PD+PB的最小值為( )
如圖,在扇形CAB中,CA=4,∠CAB=120°,D為CA的中點,P為$\widehat{BC}$上一動點(不與C,B重合),則2PD+PB的最小值為( )| A. | 4+2$\sqrt{3}$ | B. | 4$\sqrt{7}$ | C. | 10 | D. | 4$\sqrt{3}$+4 |
分析 如圖,作∥∠PAP′=120°,則AP′=2AB=8,連接PP′,BP′,則∠1=∠2,推出△APD∽△ABP′,得到BP′=2PD,于是得到2PD+PB=BP′+PB≥PP′,根據勾股定理得到PP′=$\sqrt{(2+8)^{2}+(2\sqrt{3})^{2}}$=4$\sqrt{7}$,求得2PD+PB≥4$\sqrt{7}$,于是得到結論.
解答 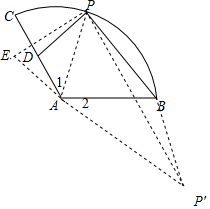 如圖,作∥∠PAP′=120°,
如圖,作∥∠PAP′=120°,
則AP′=2AB=8,連接PP′,BP′,
則∠1=∠2,
∵$\frac{AP′}{AB}$=$\frac{AP}{AD}$=2,
∴△APD∽△ABP′,
∴BP′=2PD,
∴2PD+PB=BP′+PB≥PP′,
∴PP′=$\sqrt{(2+8)^{2}+(2\sqrt{3})^{2}}$=4$\sqrt{7}$,∴2PD+PB≥4$\sqrt{7}$,
∴2PD+PB的最小值為4$\sqrt{7}$,
故選B.
點評 本題考查了軸對稱-最短距離問題,相似三角形的判定和性質,勾股定理,正確的作出輔助線是解題的關鍵.


 開心蛙狀元作業系列答案
開心蛙狀元作業系列答案 課時掌控隨堂練習系列答案
課時掌控隨堂練習系列答案 一課一練一本通系列答案
一課一練一本通系列答案 浙江之星學業水平測試系列答案
浙江之星學業水平測試系列答案科目:初中數學 來源: 題型:解答題
 如圖,已知?ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.
如圖,已知?ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | “打開電視,正在播放新聞聯播節目”是必然事件 | |
| B. | 某種彩票中獎概率為10%是指買10張一定有一張中獎 | |
| C. | 了解某種節能燈的使用壽命應采用全面檢查 | |
| D. | 一組數據3,5,4,6,7的中位數是5,方差是2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com