
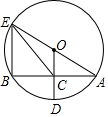
 如圖,⊙O中,半徑OD⊥弦AB于點C,連接AO并延長交⊙O于點E,連接CE、BE,AB=8,CD=2,則EC=( )
如圖,⊙O中,半徑OD⊥弦AB于點C,連接AO并延長交⊙O于點E,連接CE、BE,AB=8,CD=2,則EC=( )| A. | 5 | B. | 6 | C. | 3$\sqrt{5}$ | D. | 2$\sqrt{13}$ |
分析 設⊙O的半徑為R,由OD⊥AB,根據垂徑定理得AC=BC=$\frac{1}{2}$AB=4,在Rt△AOC中,OA=R,OC=R-CD=R-2,根據勾股定理得到(R-2)2+42=R2,解得R=5,則OC=3,由于OC為△ABE的中位線,則BE=2OC=6,再根據圓周角定理得到∠ABE=90°,然后在Rt△BCE中利用勾股定理可計算出CE.
解答 解:連結BE,設⊙O的半徑為R,如圖,
∵OD⊥AB,
∴AC=BC=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4,
在Rt△AOC中,OA=R,OC=R-CD=R-2,
∵OC2+AC2=OA2,
∴(R-2)2+42=R2,解得R=5,
∴OC=5-2=3,
∴BE=2OC=6,
∵AE為直徑,
∴∠ABE=90°,
在Rt△BCE中,CE=$\sqrt{B{C}^{2}+B{E}^{2}}$=$\sqrt{{6}^{2}+{4}^{2}}$=2$\sqrt{13}$.
故選D.
點評 本題考查了垂徑定理:平分弦的直徑平分這條弦,并且平分弦所對的兩條弧.也考查了勾股定理、圓周角定理.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,△ABC中,AB=BC,∠ABC=90°,F為AB延長線上一點,點E在BC上,且AE=CF
如圖,△ABC中,AB=BC,∠ABC=90°,F為AB延長線上一點,點E在BC上,且AE=CF查看答案和解析>>
科目:初中數學 來源: 題型:填空題
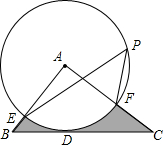 如圖,△ABC中,BC=8cm,以A為圓心,以2cm為半徑的圓與BC相切于點D,交AB于點E,交AC于點F,點P在圓上,∠EPF=50°,則圖中陰影部分的面積為8-$\frac{10}{9}$πcm2.
如圖,△ABC中,BC=8cm,以A為圓心,以2cm為半徑的圓與BC相切于點D,交AB于點E,交AC于點F,點P在圓上,∠EPF=50°,則圖中陰影部分的面積為8-$\frac{10}{9}$πcm2.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
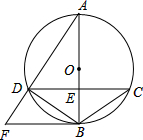 如圖,⊙O的直徑AB與弦CD交于點E,CE=DE,⊙O的切線BF與弦AD的延長線相交于點F.
如圖,⊙O的直徑AB與弦CD交于點E,CE=DE,⊙O的切線BF與弦AD的延長線相交于點F.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 方程k(x+1)(x-$\frac{3}{k}$)=-3必有實數根 | |
| B. | 若移動函數圖象使其經過原點,則只能將圖象向右移動1個單位 | |
| C. | 若k>0,則當x>0時,必有y隨著x的增大而增大 | |
| D. | 若k<0,則當x<-1時,必有y隨著x的增大而增大 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| 最高氣溫(℃) | 22 | 23 | 24 | 25 |
| 天數 | 1 | 2 | 2 | 4 |
| A. | 25,24 | B. | 24.5,25 | C. | 24,25 | D. | 23.5,24 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com