
分析 因?yàn)閮牲c(diǎn)P(p+p2+1,q)、Q(-p2+5+q,q)均在二次函數(shù)y=ax2+bx+c上,所以對稱軸x=-$\frac{b}{2a}$=$\frac{P+{p}^{2}+1-{p}^{2}+5+q}{2}$,所以-$\frac{b}{a}$=6+p+q,設(shè)方程ax2+bx+c=0的兩根為x1,3x1,則有x1+3x1=6+p+q,求出x1即可解決問題.
解答 解:兩點(diǎn)P(p+p2+1,q)、Q(-p2+5+q,q)均在二次函數(shù)y=ax2+bx+c上,
∴對稱軸x=-$\frac{b}{2a}$=$\frac{P+{p}^{2}+1-{p}^{2}+5+q}{2}$,
∴-$\frac{b}{a}$=6+p+q,設(shè)方程ax2+bx+c=0的兩根為x1,3x1,
則有x1+3x1=6+p+q,
∴x1=$\frac{6+p+q}{4}$,3x1=$\frac{18+3p+3q}{4}$,
∴方程ax2+bx+c=0的兩個根為$\frac{6+p+q}{4}$,$\frac{18+3p+3q}{4}$.
點(diǎn)評 本題考查拋物線與軸的交點(diǎn)、一元二次方程的根與系數(shù)關(guān)系等知識,解題的關(guān)鍵是靈活運(yùn)用二次函數(shù)的性質(zhì)以及根與系數(shù)關(guān)系,屬于中考創(chuàng)新題目.


 鴻圖圖書寒假作業(yè)假期作業(yè)吉林大學(xué)出版社系列答案
鴻圖圖書寒假作業(yè)假期作業(yè)吉林大學(xué)出版社系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | x≥$\sqrt{2}$ | B. | x≤$\sqrt{2}$ | C. | x<$\sqrt{2}$ | D. | x>$\sqrt{2}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
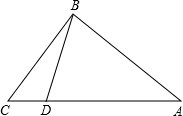 如圖,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,點(diǎn)D為AC邊上的動點(diǎn),點(diǎn)D從點(diǎn)C出發(fā),沿邊CA往A運(yùn)動,當(dāng)運(yùn)動到點(diǎn)A時停止,設(shè)點(diǎn)D運(yùn)動的時間為t秒,速度為每秒2個單位長度.
如圖,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,點(diǎn)D為AC邊上的動點(diǎn),點(diǎn)D從點(diǎn)C出發(fā),沿邊CA往A運(yùn)動,當(dāng)運(yùn)動到點(diǎn)A時停止,設(shè)點(diǎn)D運(yùn)動的時間為t秒,速度為每秒2個單位長度.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
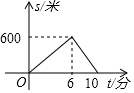 小麗、小亮從學(xué)校出發(fā)到中心書城購書,小麗步行一段時間后,小亮騎自行車沿相同路線前往,兩人均勻前行,他們的路程s(米)與小麗出發(fā)時間t(分)之間的函數(shù)關(guān)系如圖,下列說法:①小麗的速度是100米/分;②小麗出發(fā)6分鐘后小亮才出發(fā);③學(xué)校離中心書城的路程為1000米;④小亮騎車的速度是250米/分.其中正確的是( )
小麗、小亮從學(xué)校出發(fā)到中心書城購書,小麗步行一段時間后,小亮騎自行車沿相同路線前往,兩人均勻前行,他們的路程s(米)與小麗出發(fā)時間t(分)之間的函數(shù)關(guān)系如圖,下列說法:①小麗的速度是100米/分;②小麗出發(fā)6分鐘后小亮才出發(fā);③學(xué)校離中心書城的路程為1000米;④小亮騎車的速度是250米/分.其中正確的是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
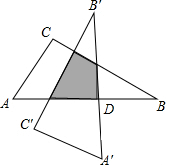 如圖,Rt△ABC中,∠C=90°,∠A=60°,AC=6,以斜邊AB的中點(diǎn)D為旋轉(zhuǎn)中心,把這個三角形按逆時針方向旋轉(zhuǎn)90°得到Rt△A′B′C′,則旋轉(zhuǎn)后兩個直角三角形重疊部分的面積為( )
如圖,Rt△ABC中,∠C=90°,∠A=60°,AC=6,以斜邊AB的中點(diǎn)D為旋轉(zhuǎn)中心,把這個三角形按逆時針方向旋轉(zhuǎn)90°得到Rt△A′B′C′,則旋轉(zhuǎn)后兩個直角三角形重疊部分的面積為( )| A. | 6 | B. | 9 | C. | 6$\sqrt{3}$ | D. | 9$\sqrt{3}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 9$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | $\frac{3}{2}$$\sqrt{3}$ | D. | $\frac{1}{4}$$\sqrt{3}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2a-a=2 | B. | 2a+b=2ab | C. | -a2b+2a2b=a2b | D. | 3a2+2a2=5a4 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | y2-49x2 | B. | $\frac{1}{49}-{x^4}$ | C. | -m2-n2 | D. | $\frac{1}{4}{(p+q)^2}-9$ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com