
 在△ABC中,AD是BC上的高,tanB=cos∠DAC.
在△ABC中,AD是BC上的高,tanB=cos∠DAC.分析 (1)由于tanB=cos∠DAC,所以根據正切和余弦的概念證明AC=BD;
(2)設AD=12k,AC=13k,然后利用題目已知條件即可解直角三角形.
解答 (1)證明:∵AD是BC上的高,
∴AD⊥BC,
∴∠ADB=90°,∠ADC=90°,
在Rt△ABD和Rt△ADC中,
∵tanB=$\frac{AD}{BD}$,cos∠DAC=$\frac{AD}{AC}$,
又∵tanB=cos∠DAC,
∴$\frac{AD}{BD}$=$\frac{AD}{AC}$,
∴AC=BD.
(2)解:在Rt△ADC中,sinC=$\frac{AD}{AC}$=$\frac{12}{13}$,
則AC=26,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=10,
∵BC=BD+CD,又AC=BD=26,
∴BC=26+10=36.
點評 此題考查解直角三角形、直角三角形的性質等知識,也考查邏輯推理能力和運算能力.


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:初中數學 來源: 題型:解答題
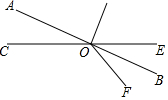 如圖所示,直線AB、CE交于O,
如圖所示,直線AB、CE交于O,查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
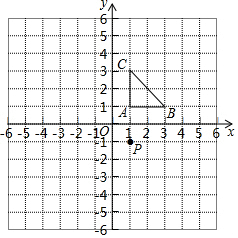 在平面直角坐標系中,小方格都是邊長為1的正方形,△ABC≌△DEF,其中點A、B、C都在格點上,請你解答下列問題:
在平面直角坐標系中,小方格都是邊長為1的正方形,△ABC≌△DEF,其中點A、B、C都在格點上,請你解答下列問題:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com