Question

4．在同圓或等圓中，如果圓心角∠BOA等于另一圓心角∠COD的2倍，則下列式子中一定成立的是（　　）

• A． AB=2CD
• B． $\widehat{AB}$=2$\widehat{CD}$
• C． $\widehat{AB}$＜2$\widehat{CD}$
• D． $\widehat{AB}$=$\widehat{CD}$

Answer 1

分析 取AB弧的中點E，連接AE、BE，如圖，利用圓心角、弧、弦的關系得到$\widehat{AB}$=2$\widehat{CD}$，所以$\widehat{AE}$=$\widehat{BE}$=$\widehat{CD}$，則AE=BE=CD，于是根據三角形三邊的關系可判斷AE+BE＞AB，所以2CD＞AB．

解答 解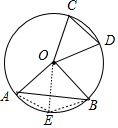：取AB弧的中點E，連接AE、BE，如圖，
∵∠AOB=2∠COD，
∴$\widehat{AB}$=2$\widehat{CD}$，
∴$\widehat{AE}$=$\widehat{BE}$=$\widehat{CD}$，
∴AE=BE=CD，
而AE+BE＞AB，
∴2CD＞AB．
故選B．

點評 本題考查了圓心角、弧、弦的關系：在同圓或等圓中，如果兩個圓心角、兩條弧、兩條弦中有一組量相等，那么它們所對應的其余各組量都分別相等．