
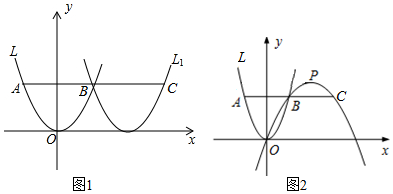
分析 (1)先確定拋物線L的解析式,根據(jù)點B的縱坐標(biāo)為2,求出A和B的坐標(biāo),計算AB的長,利用對稱性得出BC的長,所以AC=2AB=4$\sqrt{2}$;
(2)作輔助線:過B作BK⊥x軸于K,設(shè)OK=t,得出G(4t,0),設(shè)拋物線L3的解析式,并將B點的坐標(biāo)代入可求得比值.
解答  解:(1)當(dāng)a=1時,拋物線L的解析式為:y=x2,
解:(1)當(dāng)a=1時,拋物線L的解析式為:y=x2,
當(dāng)y=2時,2=x2,
∴x=±$\sqrt{2}$,
∵B在第一象限,
∴A(-$\sqrt{2}$,2),B($\sqrt{2}$,2),
∴AB=2$\sqrt{2}$,
∵向右平移拋物線L使該拋物線過點B,
∴AB=BC=2$\sqrt{2}$,
∴AC=4$\sqrt{2}$;
(2)如圖2,設(shè)拋物線L3與x軸的交點為G,其對稱軸與x軸交于Q,過B作BK⊥x軸于K,
設(shè)OK=t,則AB=BC=2t,
∴B(t,at2),
根據(jù)拋物線的對稱性得:OQ=2t,OG=2OQ=4t,
∴O(0,0),G(4t,0),
設(shè)拋物線L3的解析式為:y=a3(x-0)(x-4t),
y=a3x(x-4t),
∵該拋物線過點B(t,at2),
∴at2=a3t(t-4t),
∵t≠0,
∴a=-3a3,
∴$\frac{{a}_{3}}{a}$=-$\frac{1}{3}$,
故答案為:(1)4$\sqrt{2}$;(2)-$\frac{1}{3}$.
點評 本題是二次函數(shù)圖象與平移問題,考查了二次函數(shù)的性質(zhì)和平移的原則及二次函數(shù)的軸對稱性,解題的關(guān)鍵是理解題意,靈活運用待定系數(shù)法求函數(shù)的解析式.


科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 3a-a=3 | B. | -2(x-4)=-2x+4 | C. | -(-32)=9 | D. | 4÷$\frac{5}{4}$×$\frac{4}{5}$=4÷1=4 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
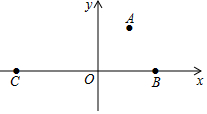 已知拋物線y=ax2+bx+2經(jīng)過A(1,$\frac{5}{4}$),B(2,0)和C三個點.
已知拋物線y=ax2+bx+2經(jīng)過A(1,$\frac{5}{4}$),B(2,0)和C三個點.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com