
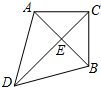
 如圖,在△ABC中,∠BAC=90°,AB=AC,BE平分∠ABC,交AC于點(diǎn)D,延長(zhǎng)BA至點(diǎn)F,連接CF,且BE⊥CF.
如圖,在△ABC中,∠BAC=90°,AB=AC,BE平分∠ABC,交AC于點(diǎn)D,延長(zhǎng)BA至點(diǎn)F,連接CF,且BE⊥CF.分析 (1)由BE⊥CF,可證得∠CBE=∠FBE,由BE=BE,∠CEB=∠FEB=90°,可證得△BCE≌△BFE,即可證得結(jié)論;
(2)由∠BAC=90°,AB=AC,BE平分∠ABC,得到∠ABC=∠ACB=45°,∠CBE=∠FBE=22.5°,進(jìn)而證得∠FCA=22.5°,于是可證得△ACF≌△ABD,由全等三角形的性質(zhì)即可證得結(jié)論.
解答 (1)∵BE平分∠ABC,BE⊥CF,
∴∠CBE=∠FBE,BE=BE,∠CEB=∠FEB=90°,
在△BCE和≌△BFE中,
$\left\{\begin{array}{l}{∠CBE=∠FBE}\\{BE=BE}\\{∠CEB=∠FBE=90°}\end{array}\right.$,
∴△BCE≌△BFE,
∴CF=CE=2;
(2)∵在△ABC中,∠BAC=90°,AB=Ac,BE平分∠ABC,
∴∠ABC=∠ACB=45°,∠CBE=∠FBE=22.5°,
由(1)知BC=BF,
∴∠BCF=∠BFC=67.5°,
∴∠FCA=22.5°,
在△ACF和△ABD中,
$\left\{\begin{array}{l}{∠FCA=∠DAB=22.5°}\\{AC=AB}\\{∠CAF=∠BAD=90°}\end{array}\right.$,
∴△ACF≌△ABD,
∴AF=AD.
點(diǎn)評(píng) 本題主要考查了角平分線的性質(zhì),全等三角形的判定與性質(zhì),等腰三角形的性質(zhì),能靈活應(yīng)用三角形的判定與性質(zhì)是解決問(wèn)題的關(guān)鍵.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
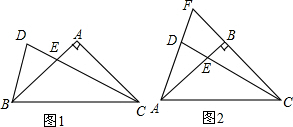
 如圖,已知△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$,△ABD是等邊三角形,求CD的長(zhǎng)度.
如圖,已知△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$,△ABD是等邊三角形,求CD的長(zhǎng)度.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
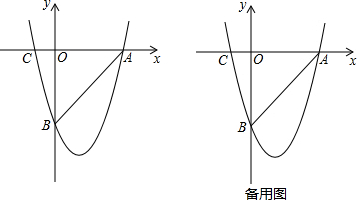
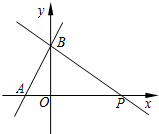 如圖,一次函數(shù)y=(m+1)x+$\frac{3}{2}$的圖象與x軸的負(fù)半軸相交于點(diǎn)A,與y軸相交于點(diǎn)B,且△OAB面積為$\frac{3}{4}$.
如圖,一次函數(shù)y=(m+1)x+$\frac{3}{2}$的圖象與x軸的負(fù)半軸相交于點(diǎn)A,與y軸相交于點(diǎn)B,且△OAB面積為$\frac{3}{4}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
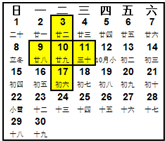 如圖是某月的日歷表,在此日歷表上可以用一個(gè)“十”字圈出5個(gè)數(shù)(如3,9,10,11,17).照此方法,若圈出的5個(gè)數(shù)中,最大數(shù)與最小數(shù)的和為46,則這5個(gè)數(shù)的和為( )
如圖是某月的日歷表,在此日歷表上可以用一個(gè)“十”字圈出5個(gè)數(shù)(如3,9,10,11,17).照此方法,若圈出的5個(gè)數(shù)中,最大數(shù)與最小數(shù)的和為46,則這5個(gè)數(shù)的和為( )| A. | 69 | B. | 84 | C. | 115 | D. | 207 |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com