
 (1)如圖,點C在線段AB上,點M,N分別是線段AC,BC的中點.
(1)如圖,點C在線段AB上,點M,N分別是線段AC,BC的中點.分析 (1)根據線段中點的性質,可得MC、CN,再根據線段的和差,可得答案;
(2)根據線段中點的性質,可得MC、CN,再根據線段的和差,可得答案;
(3)根據線段中點的性質,可得MC、CN,再根據線段的和差,可得答案.
解答 解:(1)①∵點M,N分別是線段AC,BC的中點,
∴MC=$\frac{1}{2}$AC,CN=$\frac{1}{2}$CB,
∵AC=8 cm,CB=6 cm,
∴MC=4 cm,CN=3 cm,
∴MN=7 cm;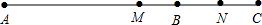
②MN=CM+CN=$\frac{1}{2}$(AB+BC)=$\frac{1}{2}$a;
故答案為:$\frac{1}{2}$a;
(2)MN=$\frac{b}{2}$,理由如下:如圖:
由M、N分別是AC、BC的中點,
得MC=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC.
由線段的和差,得MN=MC-CN=$\frac{1}{2}$AC-$\frac{1}{2}$BC=$\frac{1}{2}$(AC-BC)=$\frac{1}{2}$bcm;
故答案為:$\frac{1}{2}$b.
點評 本題考查了兩點間的距離,利用了線段中點的性質,線段的和差.


 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 方程3x-2=2x+1,移項得,3x-2x=-1+2 | |
| B. | 方程3-x=2-5( x-1),去括號得,3-x=2-5x-1 | |
| C. | 方程$\frac{2}{3}t=\frac{3}{2}$,系數化為1得,t=1 | |
| D. | 方程$\frac{x-1}{0.2}-\frac{x}{0.5}=1$,去分母得,5( x-1)-2x=1 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | 3.14 | C. | $\sqrt{\frac{4}{9}}$ | D. | $\root{3}{{\frac{1}{27}}}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
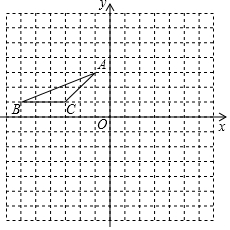 如圖,平面直角坐標系中,每個小正方形邊長都是1.
如圖,平面直角坐標系中,每個小正方形邊長都是1.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com