
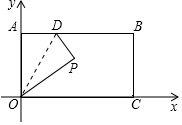
 如圖,長方形OABC的邊OC、OA分別在x軸、y軸上,點B的坐標為($\sqrt{3}$,1)點D是AB邊上一個動點(與點A不重合),沿OD將△OAD對折后,點A落到點P處,并滿足△PCB是等腰三角形,則P點坐標為($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$)或($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).
如圖,長方形OABC的邊OC、OA分別在x軸、y軸上,點B的坐標為($\sqrt{3}$,1)點D是AB邊上一個動點(與點A不重合),沿OD將△OAD對折后,點A落到點P處,并滿足△PCB是等腰三角形,則P點坐標為($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$)或($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$). 分析 連接PB,PC.分三種情況:①若PB=PC,設P(x,$\frac{1}{2}$),過P作PH⊥x軸于H.在Rt△OPH中根據勾股定理解得x,從而確定P點坐標;②若BP=BC,則BP=1,連接OB.在Rt△OBC中根據勾股定理求出OB,從而得出P為線段OB中點,求出P點坐標;③若CP=CB,則CP=1,PO=PC,P在OC中垂線上.設P($\frac{\sqrt{3}}{2}$,y),過P作PH⊥x軸于H,在Rt△OPH中根據勾股定理求出P點坐標即可.
解答  解:連接PB,PC,
解:連接PB,PC,
①若PB=PC,則P在BC的中垂線y=$\frac{1}{2}$上,
∴設P(x,$\frac{1}{2}$),
如圖,過P作PH⊥x軸于H,
在Rt△OPH中,PH=$\frac{1}{2}$,OH=x,OP=1,
∴x2+$\frac{1}{4}$=1,
解得:x1=$\frac{\sqrt{3}}{2}$,x2=-$\frac{\sqrt{3}}{2}$(不合題意),
∴P($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$);
②若BP=BC,則BP=1,連接OB,
∵OP=1,
∴OP+PB=2,
∵在Rt△OBC中,∠OCB=90°,OB=$\sqrt{3+1}$=2,
∴OP+PB=OB,
∴O,P,B三點共線,P為線段OB中點.
又∵B($\sqrt{3}$,1),
∴P($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$);
③若CP=CB,則CP=1,
∵OP=1,
∴PO=PC,則P在OC的中垂線x=$\frac{\sqrt{3}}{2}$上,
∴設P($\frac{\sqrt{3}}{2}$,y).
過P作PH⊥x軸于H,在Rt△OPH中,PH=|y|,OH=$\frac{\sqrt{3}}{2}$,OP=1,
∴y2+$\frac{3}{4}$=1,
解得:y1=$\frac{1}{2}$,y2=-$\frac{1}{2}$,
∴P($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$)或($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$),
當點P($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$)時,∠AOP=120°,此時∠AOD=60°,點D與點B重合,符合題意.
故答案為:($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$)或($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).
點評 本題是折疊問題,主要考查了矩形的性質,等腰三角形的性質以及勾股定理的運用,解決問題的關鍵是作輔助線構造直角三角形,運用分類思想進行分類討論.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 0.358×105 | B. | 3.58×104 | C. | 35.8×103 | D. | 358×102 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com