Question

10．拋物線y=ax²+bx+c（a，b，c為常數，且a≠0）經過點（-1，0）和（m，0），且1＜m＜2，當x＜-1時，y隨著x的增大而減小．下列結論①a+b＞0；②若點A（-3，y₁），點B（3，y₂）都在拋物線上，則y₁＜y₂；③a（m-1）+b=0；④若c≤-1，則b²-4ac≤4a．其中正確結論的個數是（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 利用x＜-1時，y隨著x的增大而減小可判斷拋物線開口向上，則a＞0，由于拋物線經過點（-1，0）和（m，0），且1＜m＜2，可判斷拋物線的對稱軸的位置，所以0＜-$\frac{b}{2a}$＜$\frac{1}{2}$，于是可對①進行判斷；通過比較點A到對稱軸的距離和點B到對稱軸的距離可對②進行判斷；根據二次函數圖象上點的坐標特征得到a-b+c=0，am²+bm+c=0，消去c，再因式分解得到（m+1）（m-1）+b（m-1）=0，于是可對③進行判斷；
利用拋物線頂點的縱坐標小于-1得到$\frac{4ac-{b}^{2}}{4a}$＜-1，然后利用不等式性質變形后可對④進行判斷．

解答 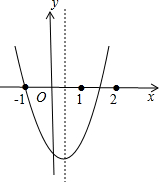解：∵拋物線過點（-1，0），當x＜-1時，y隨著x的增大而減小，
∴拋物線開口向上，
∴a＞0，
∵拋物線經過點（-1，0）和（m，0），且1＜m＜2，
∴0＜-$\frac{b}{2a}$＜$\frac{1}{2}$，
∴a+b＞0，所以①正確；
∵點A（-3，y₁），點B（3，y₂）都在拋物線上，
而點A到對稱軸的距離比點B到對稱軸的距離要大，
∴y₁＞y₂，所以②錯誤；
∵拋物線經過點（-1，0）和（m，0），
∴a-b+c=0，am²+bm+c=0，
∴am²-a+bm-b=0，即a（m+1）（m-1）+b（m+1）=0，
∴a（m-1）+b=0，所以③正確；
∵c≤-1，
∴$\frac{4ac-{b}^{2}}{4a}$＜-1，
∴b²-4ac＞4a，所以④錯誤．
故選B．

點評 本題考查了二次函數圖象與系數的關系：對于二次函數y=ax²+bx+c（a≠0），二次項系數a決定拋物線的開口方向和大小：當a＞0時，拋物線向上開口；當a＜0時，拋物線向下開口；當a與b同號時（即ab＞0），對稱軸在y軸左； 當a與b異號時（即ab＜0），對稱軸在y軸右；常數項c決定拋物線與y軸交點：拋物線與y軸交于（0，c）；拋物線與x軸交點個數由△決定：△=b²-4ac＞0時，拋物線與x軸有2個交點；△=b²-4ac=0時，拋物線與x軸有1個交點；△=b²-4ac＜0時，拋物線與x軸沒有交點．