
 如圖所示,已知AC⊥BC于C,DE⊥AB于E,AD平分∠BAC,下列結論錯誤的是( )
如圖所示,已知AC⊥BC于C,DE⊥AB于E,AD平分∠BAC,下列結論錯誤的是( )| A. | BD+DE=BC | B. | DE平分∠ADB | C. | AD平分∠EDC | D. | ED+AC>AD |
分析 根據角平分線上的點到角的兩邊的距離相等可得DE=DC,然后利用AAS證明△ACD≌△AED,再對各選項分析判斷后利用排除法.
解答 解:∵AC⊥BC,DE⊥AB,AD平分∠BAC,
∴DE=DC,
A、BD+ED=BD+DC=BC,故本選項不符合題意;
B、C、在△ACD與△AED中,
$\left\{\begin{array}{l}{∠DAC=∠DAE}\\{∠ACD=∠AED=90°}\\{AD=AD}\end{array}\right.$,
∴△ACD≌△AED(AAS),
∴∠ADC=∠ADE,
∴AD平分∠EDC,故C選項不符合題意;
但∠ADE與∠BDE不一定相等,故B選項符合題意;
D、∵△ACD≌△AED,
∴AE=AC,
∴ED+AC=ED+AE>AD(三角形任意兩邊之和大于第三邊),故本選項不符合題意.
故選B.
點評 本題考查了角平分線上的點到角的兩邊的距離相等的性質,證明△ACD≌△AED是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
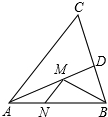 如圖,在銳角△ABC中,AB=8,∠BAC=45°,∠BAC的平分線交BC于點D,M、N分別是AD和AB上的動點,則BM+MN的最小值是( )
如圖,在銳角△ABC中,AB=8,∠BAC=45°,∠BAC的平分線交BC于點D,M、N分別是AD和AB上的動點,則BM+MN的最小值是( )| A. | 8 | B. | 6 | C. | $4\sqrt{2}$ | D. | $3\sqrt{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{a+c}{a+b}=\frac{c}{b}$ | B. | $\frac{a-c}{-a+b}=-\frac{a-c}{a+b}$ | ||
| C. | $\frac{x^8}{x^2}={x^4}$ | D. | $\frac{b}{{3{a^2}}}+\frac{1}{6ab}=\frac{{2{b^2}+a}}{{6{a^2}b}}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com