
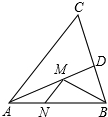
 如圖,在銳角△ABC中,AB=8,∠BAC=45°,∠BAC的平分線交BC于點D,M、N分別是AD和AB上的動點,則BM+MN的最小值是( )
如圖,在銳角△ABC中,AB=8,∠BAC=45°,∠BAC的平分線交BC于點D,M、N分別是AD和AB上的動點,則BM+MN的最小值是( )| A. | 8 | B. | 6 | C. | $4\sqrt{2}$ | D. | $3\sqrt{2}$ |
分析 作BH⊥AC,垂足為H,交AD于M′點,過M′點作M′N′⊥AB,垂足為N′,則BM′+M′N′為所求的最小值,再根據(jù)AD是∠BAC的平分線可知M′H=M′N′,再由銳角三角函數(shù)的定義即可得出結(jié)論.
解答  解:如圖,作BH⊥AC,垂足為H,交AD于M′點,過M′點作M′N′⊥AB,垂足為N′,則BM′+M′N′為所求的最小值.
解:如圖,作BH⊥AC,垂足為H,交AD于M′點,過M′點作M′N′⊥AB,垂足為N′,則BM′+M′N′為所求的最小值.
∵AD是∠BAC的平分線,
∴M′H=M′N′,
∴BH是點B到直線AC的最短距離(垂線段最短),
∵AB=8,∠BAC=45°,
∴BH=AB•sin45°=8×$\frac{\sqrt{2}}{2}$=4$\sqrt{2}$,
∵BM+MN的最小值是BM′+M′N′=BM′+M′H=BH=4$\sqrt{2}$.
故選C.
點評 本題考查的是軸對稱-最短路線問題,解答此類問題時要從已知條件結(jié)合圖形認(rèn)真思考,通過角平分線性質(zhì),垂線段最短,確定線段和的最小值.


科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2017 | B. | -2017 | C. | 2016 | D. | -2016 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
| A. | 6,16,26 | B. | 9,16,23 | C. | 15,16,17 | D. | 不確定 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 若有理數(shù)a、b在數(shù)軸上的位置如圖所示,化簡|a-b|+|2b|為( )
若有理數(shù)a、b在數(shù)軸上的位置如圖所示,化簡|a-b|+|2b|為( )| A. | a+3b | B. | a+b | C. | -a-b | D. | -a+b |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 1:1,45° | B. | $\sqrt{3}$:1,30° | C. | $\sqrt{3}$:1,45° | D. | $\sqrt{3}$:1,60° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖所示,已知AC⊥BC于C,DE⊥AB于E,AD平分∠BAC,下列結(jié)論錯誤的是( )
如圖所示,已知AC⊥BC于C,DE⊥AB于E,AD平分∠BAC,下列結(jié)論錯誤的是( )| A. | BD+DE=BC | B. | DE平分∠ADB | C. | AD平分∠EDC | D. | ED+AC>AD |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com