
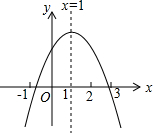 已知二次函數(shù)y=ax2+bx+c(a≠0,a、b、c為常數(shù))的圖象如圖所示,下列5個結論:①abc<0;②b<a+c;③4a+2b+c>0;④c<4b;⑤a+b<k(ka+b)(k為常數(shù),且k≠1).其中正確的結論有( )
已知二次函數(shù)y=ax2+bx+c(a≠0,a、b、c為常數(shù))的圖象如圖所示,下列5個結論:①abc<0;②b<a+c;③4a+2b+c>0;④c<4b;⑤a+b<k(ka+b)(k為常數(shù),且k≠1).其中正確的結論有( )| A. | 2個 | B. | 3個 | C. | 4個 | D. | 5個 |
分析 由拋物線的開口方向判斷a的符號,由拋物線與y軸的交點判斷c的符號,然后根據(jù)對稱軸及拋物線與x軸交點情況進行推理,進而對所得結論進行判斷.
解答 解:①由圖象可知:a<0,c>0,
∵-$\frac{b}{2a}$>0,
∴b>0,
∴abc<0,故此選項正確;
②當x=-1時,y=a-b+c<0,∴b>a+b故b<a+b,錯誤;
③由對稱知,當x=2時,函數(shù)值大于0,即y=4a+2b+c>0,故此選項正確;
④當x=3時函數(shù)值小于0,y=9a+3b+c<0,且x=-$\frac{b}{2a}$=1,
即a=-$\frac{b}{2}$,代入得9(-$\frac{b}{2}$)+3b+c<0,得c<$\frac{3}{2}$b,故∵b>0,∴c<4b此選項正確;
⑤當x=1時,y的值最大.此時,y=a+b+c,
而當x=k時,y=ak2+bk+c,
所以a+b+c>ak2+bk+c,
故a+b>ak2+bk,即a+b>k(ak+b),故此選項錯誤.
故①③④正確.
故選B.
點評 此題主要考查了圖象與二次函數(shù)系數(shù)之間的關系,二次函數(shù)y=ax2+bx+c系數(shù)符號由拋物線開口方向、對稱軸和拋物線與y軸的交點、拋物線與x軸交點的個數(shù)確定,靈活運用二次函數(shù)的性質是解題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數(shù)學 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 沒有實數(shù)根 | B. | 有一個實數(shù)根 | ||
| C. | 有兩個相等的實數(shù)根 | D. | 有兩個不相等的實數(shù)根 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題

| A. | 36π | B. | 72π | C. | 144π | D. | 18π |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
 如圖,△ABC中,AB=AC,∠A=36°,BD,CE分別平分∠ABC和∠ACB,并交于點F,則圖中全等三角形共有( )
如圖,△ABC中,AB=AC,∠A=36°,BD,CE分別平分∠ABC和∠ACB,并交于點F,則圖中全等三角形共有( )| A. | 1對 | B. | 2對 | C. | 3對 | D. | 4對 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com