
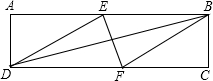
 在矩形ABCD中有一個菱形BEDF(點E、F分別在線段AB、CD上)記它們的面積分別為S矩形ABCD和S菱形BEDF,若S矩形ABCD:S菱形BFDE=(2+$\sqrt{3}$):2,給出如下結論:①AB:BE=(2+$\sqrt{3}$):2;②AE=BE;③tan∠EDF=$\frac{\sqrt{3}}{3}$;④∠FBC=60°.其中正確的結論的序號是①③④(把所有正確結論的序號都填在橫線上)
在矩形ABCD中有一個菱形BEDF(點E、F分別在線段AB、CD上)記它們的面積分別為S矩形ABCD和S菱形BEDF,若S矩形ABCD:S菱形BFDE=(2+$\sqrt{3}$):2,給出如下結論:①AB:BE=(2+$\sqrt{3}$):2;②AE=BE;③tan∠EDF=$\frac{\sqrt{3}}{3}$;④∠FBC=60°.其中正確的結論的序號是①③④(把所有正確結論的序號都填在橫線上) 分析 由圖可得矩形的寬和菱形的高相等,根據它們的面積關系即可得出AB:BE的值;根據AE:BE=(2+$\sqrt{3}$):2,可得AE=BE錯誤;由菱形的性質得出DE∥BF,DE=BE,得出∠BFC=∠EDF,由三角函數求出∠ADE=60°,得出∠ADC=∠C=90°,求出∠EDF=30°,即可得到tan∠EDF的值;根據∠BFC=30°,即可得出∠FBC=60°;最后得出正確的結論.
解答  解:如圖所示,∵S矩形ABCD:S菱形BFDE=$\frac{AB•BC}{BE•BC}$=(2+$\sqrt{3}$):2,
解:如圖所示,∵S矩形ABCD:S菱形BFDE=$\frac{AB•BC}{BE•BC}$=(2+$\sqrt{3}$):2,
∴AB:BE=(2+$\sqrt{3}$):2,
故①正確;
∵AB:BE=(2+$\sqrt{3}$):2,
∴AE:BE=$\sqrt{3}$:2,
故②錯誤;
∵四邊形BFDE是菱形,
∴DE∥BF,DE=BE,
∴∠BFC=∠EDF,
∵sin∠ADE=$\frac{AE}{DE}$=$\frac{AE}{BE}$=$\frac{\sqrt{3}}{2}$,
∴∠ADE=60°,
∵∠ADC=∠C=90°,
∴∠EDF=90°-60°=30°,
∴tan∠EDF=$\frac{\sqrt{3}}{3}$,
故③正確;
∵DE∥BF,
∴∠BFC=30°,
∴∠FBC=90°-30°=60°,
故④正確;
綜上所述,正確的結論為①③④.
故答案為:①③④.
點評 本題屬于四邊形綜合題,主要考查了矩形的性質、菱形的性質、三角函數等知識的綜合應用,熟練掌握矩形和菱形的性質,由矩形和菱形的性質得出AB:BE的值是解決問題的關鍵.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:填空題
 如圖,矩形ABCD中,BC=2,將矩形ABCD繞點D順時針旋轉90°,點A,C分別落在點A′、C′處,并且點A′,C′,B在同一條直線上,則tan∠ABA′的值為$\frac{\sqrt{5}-1}{2}$.
如圖,矩形ABCD中,BC=2,將矩形ABCD繞點D順時針旋轉90°,點A,C分別落在點A′、C′處,并且點A′,C′,B在同一條直線上,則tan∠ABA′的值為$\frac{\sqrt{5}-1}{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
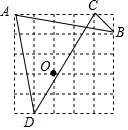 如圖為5×5的網格圖,A,B,C,D,O均在格點上,則點O是( )
如圖為5×5的網格圖,A,B,C,D,O均在格點上,則點O是( )| A. | △ACD的外心 | B. | △ABC的外心 | C. | △ACD的內心 | D. | △ABC的內心 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1.2×10-7米 | B. | 1.2×10-8米 | C. | 12×10-8米 | D. | 12×10-9米 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,O對應的有序數對為(1,3)有一個英文單詞的字母順序對應如圖中的有序數對分別為(1,2),(5,1),(5,2),(5,2),(1,3),請你把這個英文單詞寫出來或者翻譯成中文為HELLO.
如圖,O對應的有序數對為(1,3)有一個英文單詞的字母順序對應如圖中的有序數對分別為(1,2),(5,1),(5,2),(5,2),(1,3),請你把這個英文單詞寫出來或者翻譯成中文為HELLO.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com