Question

19．如圖，一塊四邊形的土地，其中∠DAB=90°，AB=4m，AD=3m，BC=12m，CD=13m，求這塊土地的面積？

Answer 1

分析 連接BD，可以求出BD的長，再根據數(shù)據的特點得出△BDC也是直角三角形，這樣四邊形的面積就被分解成了兩個直角三角形的面積之和．

解答 解：連接BD
∵AB=4m，AD=3m，∠BAD=90°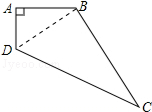
∴BD=$\sqrt{{3}^{2}+{4}^{2}}$=5（m）
∵BC=12m，CD=13m，
∴BD²+CD²=5²+12²=169，BC²=13²，
∴∠DBC=90°，
∴S_{四邊形ABCD}=S_△ABD+S_△BDC=$\frac{1}{2}$×3×4+$\frac{1}{2}$×5×12=36（m²）．

點評 本題考查了勾股定理和勾股定理的逆定理．通過作輔助線，把四邊形的面積分解成兩個直角三角形的面積來求是解本題的關鍵所在．