
 如圖,拋物線${y_1}={(x-2)^2}+m$與x軸交于點A和B,與y軸交于點C,點D是點C關于拋物線對稱軸的對稱點,若點A的坐標為(1,0),直線y2=kx+b經過點A,D.
如圖,拋物線${y_1}={(x-2)^2}+m$與x軸交于點A和B,與y軸交于點C,點D是點C關于拋物線對稱軸的對稱點,若點A的坐標為(1,0),直線y2=kx+b經過點A,D.分析 (1)把點A的坐標代入拋物線解析式可求出m的值,進而可得到拋物線的解析式;
(2)首先由拋物線的解析式可求出點C的坐標,再根據函數圖象的對稱性即可求出點D的坐標;由于點A的坐標已知,進而可求出直線AD的解析式;
(3)結合兩個函數圖象可知當但直線在拋物線上方時可得到y2>y1的解集.
解答 解:
(1)∵點A(1,0)在拋物線上,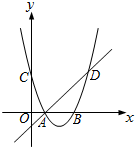
∴(1-2)2+m=0,
∴m=-1,
∴y1=(x-2)2-1;
(2)拋物線y1=(x-2)2-1的對稱軸為x=2,與y的交點C的坐標為(0,3),
∵點D是點C關于對稱軸x=2的對稱點,
∴點D的坐標為(4,3),
直線AD經過點點A,D,
∴$\left\{{\begin{array}{l}{k+b=0}\\{4k+b=3}\end{array}}\right.$,
解得k=1,b=-1,
∴y=x-1;
(3)當1<x<4時,y2>y1.
點評 本題考查二次函數與不等式(組)的知識,同時涉及到用待定系數法求一次函數解析式和二次函數的性質,解題要注意數形結合思想的靈活運用,難度一般.


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:初中數學 來源: 題型:解答題
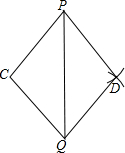 如圖,已知△PCQ,按如下步驟作圖:①以P為圓心,PC長為半徑畫弧;②以Q為圓心,QC長為半徑畫弧,兩弧相交于點D;③連接PD、QD.求證:△PCQ≌△PDQ.
如圖,已知△PCQ,按如下步驟作圖:①以P為圓心,PC長為半徑畫弧;②以Q為圓心,QC長為半徑畫弧,兩弧相交于點D;③連接PD、QD.求證:△PCQ≌△PDQ.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,OC為∠AOB內一條直線,下列條件中不能確定OC平分∠AOB的是( )
如圖,OC為∠AOB內一條直線,下列條件中不能確定OC平分∠AOB的是( )| A. | ∠AOC=∠BOC | B. | ∠AOB=2∠AOC | C. | ∠AOC+∠COB=∠AOB | D. | $∠BOC=\frac{1}{2}∠AOB$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1022.01(精確到0.01) | B. | 1022(精確到個位) | ||
| C. | 1022.00(精確到0.1) | D. | 1022.010(精確到千分位) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com