
分析 因為x為有理數,所以要分類討論x-1與x+2的正負,再去掉絕對值符號再計算.
解答 解:因為x為有理數,就是說x可以為正數,也可以為負數,也可以為0,所以要分情況討論.
(1)當x<-2時,x-1<0,x+2<0,所以|x-1|+|x+2|=-(x-1)-(x+2)=-2x-1>3;
(2)當-2≤x<1時,x-1<0,x+2≥0,所以|x-1|+|x+2|=-(x-1)+(x+2)=3;
(3)當x≥1時,x-1≥0,x+2>0,所以|x-1|+|x+2|=(x-1)+(x+2)=2x+1≥3;
綜上所述,所以|x-1|+|x+2|的最小值是3.
故答案為:3.
點評 本題考查了絕對值和代數式求值的知識,注意絕對值的運算,應先判斷絕對值里面的數是負數還是非負數,再去絕對值,最后進行運算.解答此題時要注意分類討論不要漏解.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
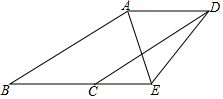 已知如圖,∠ABC=∠ADC,AB∥CD,AE平分∠BAD,當∠ADC:∠CDE=3:2,且∠AED=60°時,求∠BED的度數為$\frac{960}{7}$度.
已知如圖,∠ABC=∠ADC,AB∥CD,AE平分∠BAD,當∠ADC:∠CDE=3:2,且∠AED=60°時,求∠BED的度數為$\frac{960}{7}$度.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
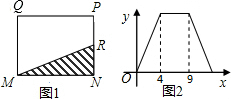
| A. | M處 | B. | N處 | C. | P處 | D. | Q處 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
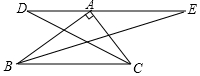 如圖,在△ABC中,∠BAC=90°,AC=6,BC=10,過點A的直線DE∥BC,∠ABC與∠ACB的平分線分別交DE于E,D,求DE的長.
如圖,在△ABC中,∠BAC=90°,AC=6,BC=10,過點A的直線DE∥BC,∠ABC與∠ACB的平分線分別交DE于E,D,求DE的長.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com