
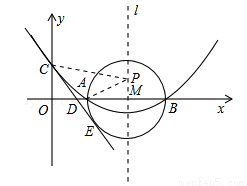
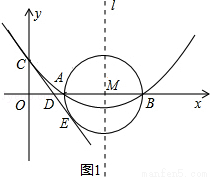
(12分)如圖,已知拋物線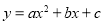 (
(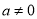 )的頂點坐標為(4,
)的頂點坐標為(4,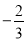 ),且與y軸交于點C(0,2),與x軸交于A、B兩點(點A在點B的左邊).
),且與y軸交于點C(0,2),與x軸交于A、B兩點(點A在點B的左邊).
(1)求拋物線的解析式及A、B兩點的坐標;
(2)在(1)中拋物線的對稱軸l上是否存在一點P,使AP+CP的值最小,若存在,求AP+CP的最小值;若不存在,請說明理由;
(3)在以AB為直徑的⊙M中,CE與⊙M相切于點E,CE交x軸于點D,求直線CE的解析式.
(1)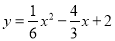 ,A(2,0)B(6,0);(2)存在,
,A(2,0)B(6,0);(2)存在,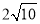 ;(3)
;(3)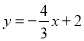 .
.
【解析】
試題分析:(1)利用頂點式求得二次函數的解析式后令其等于0后求得x的值即為與x軸交點坐標的橫坐標;
(2)線段BC的長即為AP+CP的最小值;
(3)連接ME,根據CE是⊙M的切線得到ME⊥CE,∠CEM=90°,從而證得△COD≌△MED,設OD=x,在RT△COD中,利用勾股定理求得x的值即可求得點D的坐標,然后利用待定系數法確定線段CE的解析式即可.
試題解析:(1)由題意,設拋物線的解析式為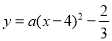 (
(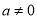 ),∵拋物線經過(0,2),∴
),∵拋物線經過(0,2),∴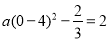 ,解得:
,解得: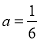 ,∴
,∴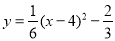 ,即:
,即: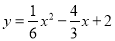 ,當
,當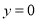 時,
時,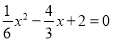 ,解得:
,解得: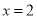 或
或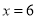 ,∴A(2,0),B(6,0);
,∴A(2,0),B(6,0);
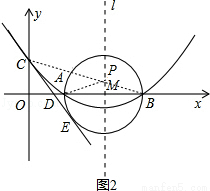
(2)存在,如圖2,由(1)知:拋物線的對稱軸l為x=4,因為A、B兩點關于l對稱,連接CB交l于點P,則AP=BP,所以AP+CP=BC的值最小.∵B(6,0),C(0,2),∴OB=6,OC=2,∴BC=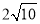 ,∴AP+CP=BC=
,∴AP+CP=BC=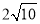 ,∴AP+CP的最小值為
,∴AP+CP的最小值為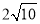 ;
;
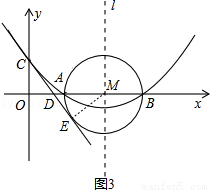
(3)如圖3,連接ME,∵CE是⊙M的切線,∴ME⊥CE,∠CEM=90°,∵C的坐標(0,2),∴OC=2,∵AB=4,∴ME=2,∴OC=ME=2,∵∠ODC=∠MDE,在△COD與△MED中,∵∠COD=∠MED,∠ODC=∠EDM,OC=ME,∴△COD≌△MED(AAS),∴OD=DE,DC=DM,設OD=x,則CD=DM=OM﹣OD=4﹣x,則Rt△COD中, 2,∴
2,∴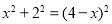 ,∴
,∴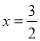 ,∴D(
,∴D(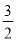 ,0),設直線CE的解析式為
,0),設直線CE的解析式為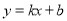 (
(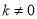 ),∵直線CE過C(0,2),D(
),∵直線CE過C(0,2),D(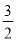 ,0)兩點,則
,0)兩點,則 ,解得:
,解得: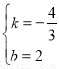 ,∴直線CE的解析式為
,∴直線CE的解析式為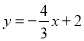 .
.
考點:二次函數綜合題.


 名校提分一卷通系列答案
名校提分一卷通系列答案 課程達標測試卷闖關100分系列答案
課程達標測試卷闖關100分系列答案 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案 全能闖關100分系列答案
全能闖關100分系列答案科目:初中數學 來源:2014-2015學年江蘇省九年級上學期期中調研考試數學試卷(解析版) 題型:解答題
(本題滿分13分)在平面直角坐標系 中,點M(
中,點M( ,
, ),以點M為圓心,OM長為半徑作⊙M ,使⊙M與直線OM的另一交點為點B,與x軸、y軸的另一交點分別為點D,A(如圖),連接AM點P是弧AB上的動點.
),以點M為圓心,OM長為半徑作⊙M ,使⊙M與直線OM的另一交點為點B,與x軸、y軸的另一交點分別為點D,A(如圖),連接AM點P是弧AB上的動點.

(1)寫出∠AMB的度數;
(2)點Q在射線OP上,且OP·OQ=20,過點Q作QC垂直于直線OM,垂足為C,直線QC交x軸于點E.
①當動點P與點B重合時,求點E的坐標;
②連接QD,設點Q的縱坐標為t,△QOD的面積為S,求S與t的函數關系式及S的取值范圍.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省九年級上學期期中調研考試數學試卷(解析版) 題型:選擇題
如圖,一個半徑為r的圓形紙片在邊長為 (
( )的等邊三角形內任意運動,則在該等邊三角形內,這個圓形紙片“不能接觸到的部分”的面積是( )
)的等邊三角形內任意運動,則在該等邊三角形內,這個圓形紙片“不能接觸到的部分”的面積是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省九年級上學期期中調研考試數學試卷(解析版) 題型:選擇題
如圖,點A、B、P為⊙O上的點,若∠PBO=15°,且PA∥OB,則∠AOB=( )
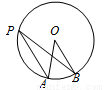
A.15° B.20° C.30° D.45°
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省九年級上學期期中考試數學試卷(解析版) 題型:解答題
(8分)如圖. ABCD中,AB=4,點D的坐標是(0,8),以點C為頂點的拋物線
ABCD中,AB=4,點D的坐標是(0,8),以點C為頂點的拋物線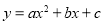 經過x軸上的點A、B.
經過x軸上的點A、B.
(1)求拋物線的解析式;
(2)寫出x為何值時,函數值小于0.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省九年級上學期期中考試數學試卷(解析版) 題型:填空題
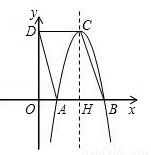
如圖,AB是⊙O的弦,AC是⊙O的切線,A為切點,BC經過圓心.若∠B=25o,則∠C的大小等于______________.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年黑龍江省伊春市九年級11月月考數學試卷(解析版) 題型:解答題
(8分)
如圖所示,在平面直角坐標系中,拋物線 (
( )經過A(-1,0)、B(3,0)兩點,拋物線與y軸交點為C,其頂點為D,連接BD,點P是線段BD上一個動點(不與B,D重合),過點P作y軸的垂線,垂足為E,連接BE.
)經過A(-1,0)、B(3,0)兩點,拋物線與y軸交點為C,其頂點為D,連接BD,點P是線段BD上一個動點(不與B,D重合),過點P作y軸的垂線,垂足為E,連接BE.

(1)求拋物線的解析式,并寫出頂點D的坐標;
(2)如果P點的坐標為( ,
, ),△PBE的面積為
),△PBE的面積為 ,求
,求 與
與 的函數關系式,寫出自變量
的函數關系式,寫出自變量 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com