
(本題滿分13分)在平面直角坐標系 中,點M(
中,點M( ,
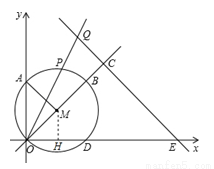
, ),以點M為圓心,OM長為半徑作⊙M ,使⊙M與直線OM的另一交點為點B,與x軸、y軸的另一交點分別為點D,A(如圖),連接AM點P是弧AB上的動點.
),以點M為圓心,OM長為半徑作⊙M ,使⊙M與直線OM的另一交點為點B,與x軸、y軸的另一交點分別為點D,A(如圖),連接AM點P是弧AB上的動點.

(1)寫出∠AMB的度數;
(2)點Q在射線OP上,且OP·OQ=20,過點Q作QC垂直于直線OM,垂足為C,直線QC交x軸于點E.
①當動點P與點B重合時,求點E的坐標;
②連接QD,設點Q的縱坐標為t,△QOD的面積為S,求S與t的函數關系式及S的取值范圍.
(1)90°;(2)①(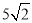 ,0);②S=
,0);②S=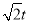 ,5≤S≤10.
,5≤S≤10.
【解析】
試題分析:(1)首先過點M作MH⊥OD于點H,由點M(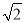 ,
,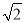 ),可得∠MOH=45°,OH=MH=
),可得∠MOH=45°,OH=MH=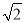 ,繼而求得∠AOM=45°,又由OM=AM,可得△AOM是等腰直角三角形,繼而可求得∠AMB的度數;
,繼而求得∠AOM=45°,又由OM=AM,可得△AOM是等腰直角三角形,繼而可求得∠AMB的度數;
(2)①由OH=MH=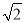 ,MH⊥OD,即可求得OD與OM的值,繼而可得OB的長,又由動點P與點B重合時,OP•OQ=20,可求得OQ的長,繼而求得答案;
,MH⊥OD,即可求得OD與OM的值,繼而可得OB的長,又由動點P與點B重合時,OP•OQ=20,可求得OQ的長,繼而求得答案;
②由OD=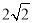 ,Q的縱坐標為t,即可得S=
,Q的縱坐標為t,即可得S=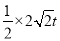 =
=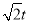 ,然后分別從當動點P與B點重合時,過點Q作QF⊥x軸,垂足為F點,與當動點P與A點重合時,Q點在y軸上,去分析求解即可求得答案.
,然后分別從當動點P與B點重合時,過點Q作QF⊥x軸,垂足為F點,與當動點P與A點重合時,Q點在y軸上,去分析求解即可求得答案.
試題解析:(1)過點M作MH⊥OD于點H,∵點M(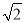 ,
,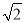 ),∴OH=MH=
),∴OH=MH=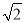 ,∴∠MOD=45°,∵∠AOD=90°,∴∠AOM=45°,∵OM=AM,∴∠OAM=∠AOM=45°,∴∠AMO=90°,∴∠AMB=90°;
,∴∠MOD=45°,∵∠AOD=90°,∴∠AOM=45°,∵OM=AM,∴∠OAM=∠AOM=45°,∴∠AMO=90°,∴∠AMB=90°;
(2)①∵OH=MH=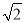 ,MH⊥OD,∴OM=
,MH⊥OD,∴OM=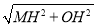 =2,OD=2OH=
=2,OD=2OH=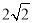 ,∴OB=4,∵動點P與點B重合時,OP•OQ=20,∴OQ=5,∵∠OQE=90°,∠POE=45°,∴OE=
,∴OB=4,∵動點P與點B重合時,OP•OQ=20,∴OQ=5,∵∠OQE=90°,∠POE=45°,∴OE=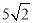 ,∴E點坐標為(
,∴E點坐標為(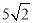 ,0);
,0);
②∵OD=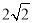 ,Q的縱坐標為t,∴S=
,Q的縱坐標為t,∴S=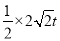 =
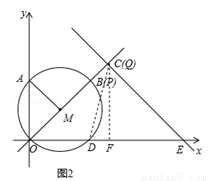
=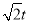 ,如圖2,當動點P與B點重合時,過點Q作QF⊥x軸,垂足為F點,∵OP=4,OP•OQ=20,∴OQ=5,∵∠OFC=90°,∠QOD=45°,∴t=QF=
,如圖2,當動點P與B點重合時,過點Q作QF⊥x軸,垂足為F點,∵OP=4,OP•OQ=20,∴OQ=5,∵∠OFC=90°,∠QOD=45°,∴t=QF=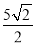 ,此時S=
,此時S=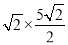 =5;
=5;
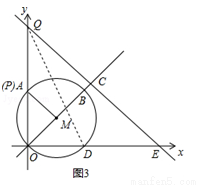
如圖3,當動點P與A點重合時,Q點在y軸上,∴OP=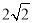 ,∵OP•OQ=20,∴t=OQ=
,∵OP•OQ=20,∴t=OQ=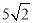 ,此時S=
,此時S=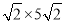 =10;∴S的取值范圍為5≤S≤10.
=10;∴S的取值范圍為5≤S≤10.
考點:圓的綜合題.


科目:初中數學 來源: 題型:單選題
能判定四邊形ABCD是平行四邊形的是( )
| A.AB∥CD,AD=BC | B.∠A=∠B,∠C=∠D |
| C.AB=CD,AD=BC | D.AB=AD,BC=CD |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,AC是⊙o的直徑,PA切⊙o于點A,點B是⊙o上的-點,且∠BAC=30°,∠APB=60°。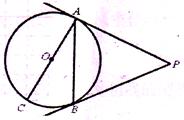
(1)求證:PB是⊙o的切線;
(2)若⊙o的半徑為2,求弦AB及PA、PB的長。
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省九年級上學期期中調研考試數學試卷(解析版) 題型:填空題
(本題滿分10分)在不透明的袋子中有四張標著數字1,2,3,4的卡片,小明、小華兩人按照各自的規則玩抽卡片游戲.
小明畫出樹狀圖如圖所示:
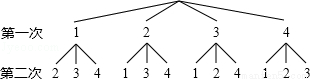
小華列出表格如下:
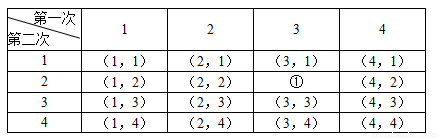
回答下列問題:
(1)根據小明畫出的樹形圖分析,他的游戲規則是,隨機抽出一張卡片后 (填“放回”或“不放回”),再隨機抽出一張卡片;
(2)根據小華的游戲規則,表格中①表示的有序數對為 ;
(3)規定兩次抽到的數字之和為奇數的獲勝,你認為誰獲勝的可能性大?為什么?
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省九年級上學期期中考試數學試卷(解析版) 題型:解答題
(12分)如圖,已知拋物線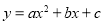 (
(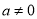 )的頂點坐標為(4,
)的頂點坐標為(4,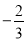 ),且與y軸交于點C(0,2),與x軸交于A、B兩點(點A在點B的左邊).
),且與y軸交于點C(0,2),與x軸交于A、B兩點(點A在點B的左邊).
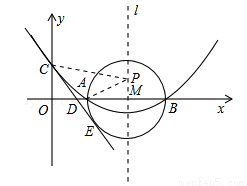
(1)求拋物線的解析式及A、B兩點的坐標;
(2)在(1)中拋物線的對稱軸l上是否存在一點P,使AP+CP的值最小,若存在,求AP+CP的最小值;若不存在,請說明理由;
(3)在以AB為直徑的⊙M中,CE與⊙M相切于點E,CE交x軸于點D,求直線CE的解析式.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年黑龍江省伊春市九年級11月月考數學試卷(解析版) 題型:選擇題
下列圖形中,既是軸對稱圖形又是中心對稱圖形的是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com