
 如圖,D是△ABC的斜邊BC上一點,DE⊥AB,DF⊥AC,EF是垂足,四邊形AEDF的面積為y,BD為x.y與x的函數關系圖象正確的是( )
如圖,D是△ABC的斜邊BC上一點,DE⊥AB,DF⊥AC,EF是垂足,四邊形AEDF的面積為y,BD為x.y與x的函數關系圖象正確的是( )| A. |  | B. |  | C. |  | D. |  |
分析 設BC=a,AB=c,AC=b,先證明△BDE∽△BCA,錄用相似比可表示出DE=$\frac{b}{a}$x,利用同樣方法得到DF=$\frac{c}{a}$(a-x),則根據矩形的面積公式得到y=-$\frac{bc}{{a}^{2}}$x2+$\frac{bc}{a}$x(0<x<a),于是得到y與x的函數圖象為開口向下的拋物線,由此特征可對各選項進行判斷.
解答 解:設BC=a,AB=c,AC=b,
∵DE⊥AB,
∴∠DEB=90°,
而∠DBE=∠CBA,
∴△BDE∽△BCA,
∴DE:CA=BD:BC,
∴DE=$\frac{b}{a}$x,
同理可得DF=$\frac{c}{a}$(a-x),
∴y=$\frac{b}{a}$x•$\frac{c}{a}$(a-x)=-$\frac{bc}{{a}^{2}}$x2+$\frac{bc}{a}$x(0<x<a).
故選B.
點評 本題考查了動點問題的函數圖象:函數圖象是典型的數形結合,圖象應用信息廣泛,通過看圖獲取信息,不僅可以解決生活中的實際問題,還可以提高分析問題、解決問題的能力.解決本題的關鍵是利用相似比用x表示出DE和DF.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系中,△ABC的三個頂點都在格點上,點A的坐標為(2,4),請解答下列問題:
如圖,在平面直角坐標系中,△ABC的三個頂點都在格點上,點A的坐標為(2,4),請解答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
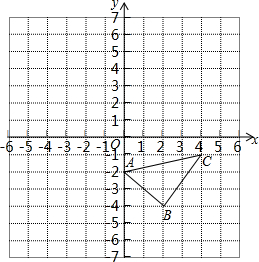 如圖,在平面直角坐標系中,△ABC的三個頂點均在格點上.
如圖,在平面直角坐標系中,△ABC的三個頂點均在格點上.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,P是⊙O外一動點,PA、PB、CD是⊙O的三條切線,C、D分別在PA、PB上,連接OC、OD.設∠P為x°,∠COD為y°,則y隨x的函數關系圖象為( )
如圖,P是⊙O外一動點,PA、PB、CD是⊙O的三條切線,C、D分別在PA、PB上,連接OC、OD.設∠P為x°,∠COD為y°,則y隨x的函數關系圖象為( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 某次火災事故中,消防員架起一架AB=25米長的云梯.如圖斜靠在一面墻上,梯子底端B離墻7米.
某次火災事故中,消防員架起一架AB=25米長的云梯.如圖斜靠在一面墻上,梯子底端B離墻7米.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,直線y=-2x+7與x軸、y軸分別相交于點C、B,與直線y=$\frac{3}{2}$x相交于點A.
如圖,直線y=-2x+7與x軸、y軸分別相交于點C、B,與直線y=$\frac{3}{2}$x相交于點A.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com