
 如圖,AB、AC是⊙O的切線,B、C為切點,過點O作AB的平行線交AC于點D,DE⊥AB于點E.
如圖,AB、AC是⊙O的切線,B、C為切點,過點O作AB的平行線交AC于點D,DE⊥AB于點E.分析 (1)結論:四邊形ODEB是矩形.首先證明四邊形ODEB是平行四邊形,再證明∠OBE=90°即可.
(2)結論:DA′是⊙O的切線,作OK⊥DA′于K.理由角平分線的性質定理,只要證明OK=OC即可.
(3)四邊形ODEB是矩形,推出EB=OD,DE=OB,∠DEB=∠DEA=90°,設OD=EB=x,在Rt△ADE中,∵AD=5,tanA=$\frac{4}{3}$,推出DE=OB=OC=4,AE=3,由AC、AB是切線,推出AC=AB=3+x,CD=3+x-5=x-2,在Rt△CDO中,根據CD2+OC2=DO2列出方程求出x即可解決問題.
解答 解:(1)四邊形ODEB是矩形.
理由:∵AB是切線,
∴OB⊥AB,∵DE⊥AB,
∴DE∥OB,
∵OD∥AB,
∴四邊形ODEB是平行四邊形,
∵∠OBE=90°,
∴四邊形ODEB是矩形.
(2)結論:DA′是⊙O的切線,
理由:作OK⊥DA′于K.
∵DA沿DE翻折后對應線段為DA′,
∴∠ADE=∠A′DE,
∵四邊形ODEB是矩形,
∴∠ODE=90°,
∴∠ODK+∠EDK=90°,∠ADE+∠CDO=90°,
∴∠ODC=∠ODK,
∵AC 是⊙O切線,
∴OC⊥DC,∵OK⊥DK,
∴OK=OC,
∴DA′是⊙O的切線.
(3)∵四邊形ODEB是矩形,
∴EB=OD,DE=OB,∠DEB=∠DEA=90°,設OD=EB=x,
在Rt△ADE中,∵AD=5,tanA=$\frac{4}{3}$,
∴DE=OB=OC=4,AE=3,
∵AC、AB是切線,
∴AC=AB=3+x,CD=3+x-5=x-2,
在Rt△CDO中,∵CD2+OC2=DO2,
∴(x-2)2+42=x2,
∴x=5,
∴AB=AC=8,CO=OB=4,
∴四邊形ABOC的周長為24.
故答案為24.
點評 本題考查圓綜合題、矩形的判定和性質、切線的判定和性質、勾股定理等知識,解題的關鍵是學會添加常用輔助線,學會用方程的思想思考問題,屬于中考壓軸題.


科目:初中數學 來源: 題型:填空題
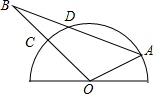 如圖,半圓O是一個量角器,△AOB為一紙片,AB交半圓于點D,OB交半圓于點C,若點C、D、A在量角器上對應讀數分別為45°,70°,150°,則∠AOB的度數為105°;∠A的度數為50°.
如圖,半圓O是一個量角器,△AOB為一紙片,AB交半圓于點D,OB交半圓于點C,若點C、D、A在量角器上對應讀數分別為45°,70°,150°,則∠AOB的度數為105°;∠A的度數為50°.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
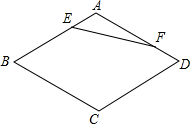 如圖,在菱形ABCD中,∠B=60°,AB=a,點E,F分別是邊AB,AD上的動點,且AE+AF=a,則線段EF的最小值為$\frac{\sqrt{3}}{2}$a.
如圖,在菱形ABCD中,∠B=60°,AB=a,點E,F分別是邊AB,AD上的動點,且AE+AF=a,則線段EF的最小值為$\frac{\sqrt{3}}{2}$a.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | msin40° | B. | mcos40° | C. | mtan40° | D. | $\frac{m}{tan40°}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 處于中間位置的數為這組數的中位數 | |
| B. | 中間兩個數的平均數為這組數的中位數 | |
| C. | 想要了解一批電磁爐的使用壽命,適合采用全面調查的方法 | |
| D. | 公司員工月收入的眾數是3500元,說明該公司月收入為3500元的員工最多 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
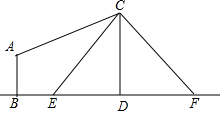 如圖,電線桿CD上的C處引拉線CE,CF固定電線桿,在離電線桿6米的B處安置測角儀(點B,E,D在同一直線上),在A處測得電線桿上C處的仰角為30°,已知測角儀的高AB=1.5米,BE=2.3米,求拉線CE的長,(精確到0.1米)參考數據$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73.
如圖,電線桿CD上的C處引拉線CE,CF固定電線桿,在離電線桿6米的B處安置測角儀(點B,E,D在同一直線上),在A處測得電線桿上C處的仰角為30°,已知測角儀的高AB=1.5米,BE=2.3米,求拉線CE的長,(精確到0.1米)參考數據$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
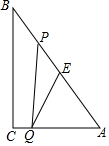 如圖,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.點P從 B出發沿BA向A運動,速度為每秒1cm,點E是點B以P為對稱中心的對稱點,點P運動的同時,點Q從A出發沿AC向C運動,速度為每秒2cm,當 點Q到達頂點C時,P,Q同時停止運動,設P,Q兩點運動時間為t秒.
如圖,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.點P從 B出發沿BA向A運動,速度為每秒1cm,點E是點B以P為對稱中心的對稱點,點P運動的同時,點Q從A出發沿AC向C運動,速度為每秒2cm,當 點Q到達頂點C時,P,Q同時停止運動,設P,Q兩點運動時間為t秒.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com