
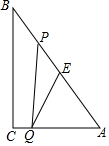
 如圖,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.點P從 B出發沿BA向A運動,速度為每秒1cm,點E是點B以P為對稱中心的對稱點,點P運動的同時,點Q從A出發沿AC向C運動,速度為每秒2cm,當 點Q到達頂點C時,P,Q同時停止運動,設P,Q兩點運動時間為t秒.
如圖,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.點P從 B出發沿BA向A運動,速度為每秒1cm,點E是點B以P為對稱中心的對稱點,點P運動的同時,點Q從A出發沿AC向C運動,速度為每秒2cm,當 點Q到達頂點C時,P,Q同時停止運動,設P,Q兩點運動時間為t秒.分析 (1)先在Rt△ABC中,由勾股定理求出AB=10,再由BP=t,AQ=2t,得出AP=10-t,然后由PQ∥BC,根據平行線分線段成比例定理得出$\frac{AP}{AB}=\frac{AQ}{AC}$,列出比例式=$\frac{10-t}{10}=\frac{2t}{6}$,求解即可;
(2)根據S四邊形PQCB=S△ACB-S△APQ=$\frac{1}{2}$AC•BC-$\frac{1}{2}$AP•AQ•sinA,即可得出y關于t的函數關系式;根據四邊形PQCB面積是△ABC面積的$\frac{3}{5}$,列出方程$\frac{4}{5}$t2-8t+24=$\frac{3}{4}$×24,解方程即可;
(3)△AEQ為等腰三角形時,分三種情況討論:①AE=AQ;②EA=EQ;③QA=QE,每一種情況都可以列出關于t的方程,解方程即可.
解答 解:(1)Rt△ABC中,∵∠C=90°,BC=8cm,AC=6cm,
∴AB=10cm.
∵BP=t,AQ=2t,
∴AP=AB-BP=10-t.
∵PQ∥BC,
∴$\frac{AP}{AB}=\frac{AQ}{AC}$,
∴$\frac{10-t}{10}=\frac{2t}{6}$,
解得t=$\frac{30}{13}$;
(2)∵S四邊形PQCB=S△ACB-S△APQ=$\frac{1}{2}$AC•BC-$\frac{1}{2}$AP•AQ•sinA
∴y=$\frac{1}{2}$×6×8-$\frac{1}{2}$×(10-t)•2t•$\frac{8}{10}$=24-$\frac{4}{5}$t(10-t)
=$\frac{4}{5}$t2-8t+24,
即y關于t的函數關系式為y=$\frac{4}{5}$t2-8t+24;
∵四邊形PQCB面積能是△ABC面積的$\frac{3}{5}$,
∴$\frac{4}{5}$t2-8t+24=$\frac{3}{5}$×24,
整理,得t2-10t+12=0,
解得t1=5-$\sqrt{13}$,t2=5+$\sqrt{13}$(不合題意舍去).
故四邊形PQCB面積能是△ABC面積的$\frac{3}{5}$,此時t的值為5-$\sqrt{13}$;
(3)△AEQ為等腰三角形時,分三種情況討論:
①如果AE=AQ,那么10-2t=2t,解得t=$\frac{5}{2}$;
②如果EA=EQ,那么(10-2t)×$\frac{6}{10}$=t,解得t=$\frac{30}{11}$;
③如果QA=QE,那么2t×$\frac{6}{10}$=5-t,解得t=$\frac{25}{11}$.
故當t為$\frac{5}{2}$秒$\frac{30}{11}$秒$\frac{25}{11}$秒時,△AEQ為等腰三角形.
點評 此題是幾何變換綜合題,主要考查了勾股定理,平行線的判定,四邊形的面積,等腰三角形的判定,中心對稱的性質,綜合性較強,難度適中.運用分類討論、方程思想是解題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
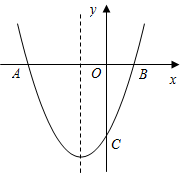 已知:拋物線的對稱軸為x=-1,與x軸交于A,B兩點,與y軸交于點C,其中A(-3,0)、C(0,-2).
已知:拋物線的對稱軸為x=-1,與x軸交于A,B兩點,與y軸交于點C,其中A(-3,0)、C(0,-2).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,AB、AC是⊙O的切線,B、C為切點,過點O作AB的平行線交AC于點D,DE⊥AB于點E.
如圖,AB、AC是⊙O的切線,B、C為切點,過點O作AB的平行線交AC于點D,DE⊥AB于點E.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
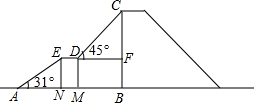 如圖,是某兒童樂園為小朋友設計的滑梯平面圖.已知BC=5米,AB=8米,中間平臺寬度DE=1米,EN、DM、CB為三根垂直于AB的支柱,垂足分別為N、M、B,∠EAB=31°,DF⊥BC于F,∠CDF=45°.求DM和BC的水平距離BM的長度.(結果精確到0.1米,參考數據:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
如圖,是某兒童樂園為小朋友設計的滑梯平面圖.已知BC=5米,AB=8米,中間平臺寬度DE=1米,EN、DM、CB為三根垂直于AB的支柱,垂足分別為N、M、B,∠EAB=31°,DF⊥BC于F,∠CDF=45°.求DM和BC的水平距離BM的長度.(結果精確到0.1米,參考數據:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com