
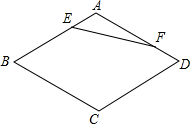
 如圖,在菱形ABCD中,∠B=60°,AB=a,點E,F(xiàn)分別是邊AB,AD上的動點,且AE+AF=a,則線段EF的最小值為$\frac{\sqrt{3}}{2}$a.
如圖,在菱形ABCD中,∠B=60°,AB=a,點E,F(xiàn)分別是邊AB,AD上的動點,且AE+AF=a,則線段EF的最小值為$\frac{\sqrt{3}}{2}$a. 分析 由在邊長為a的菱形ABCD中,易得△ABC、△CAD都是邊長為a的正三角形,繼而證得△ACE≌△DCF,繼而證得△CEF是正三角形,繼而可得當動點E運動到點B或點A時,CE的值最大,當CE⊥AB,即E為AB的中點時,EF的值最小.
解答 解:連接AC、CE、CF,如圖所示: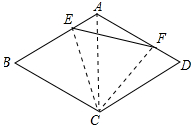
∵四邊形ABCD是邊長為a的菱形,∠B=60°,
∴△ABC、△CAD都是邊長為a的正三角形,
∴AB=BC=CD=AC=AD,∠CAE=∠ACB=∠ACD=∠CDF=60°,
∵AE+AF=a,
∴AE=a-AF=AD-AF=DE,
在△ACE和△DCF中,$\left\{\begin{array}{l}{AE=DF}&{\;}\\{∠CAE=∠CDF}&{\;}\\{AC=DC}&{\;}\end{array}\right.$,
∴△ACE≌△DCF(SAS),
∴∠ACE=∠DCF,
∴∠ACE+∠ACF=∠DCF+∠ACF,
∴∠ECF=∠ACD=60°,
∴△CEF是正三角形,
∴EF=CE=CF,
當動點E運動到點B或點A時,CE的最大值為a,
當CE⊥AB,即E為BD的中點時,CE的最小值為$\frac{\sqrt{3}}{2}$a,
∵EF=CE,
∴EF的最小值為$\frac{\sqrt{3}}{2}$a.
故答案為:$\frac{\sqrt{3}}{2}$a.
點評 此題考查了菱形的性質(zhì)、等邊三角形的判定與性質(zhì)以及全等三角形的判定與性質(zhì).注意證得△ACE≌△DCF是解此題的關(guān)鍵.


科目:初中數(shù)學 來源: 題型:解答題
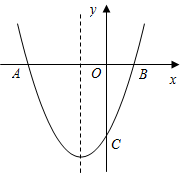 已知:拋物線的對稱軸為x=-1,與x軸交于A,B兩點,與y軸交于點C,其中A(-3,0)、C(0,-2).
已知:拋物線的對稱軸為x=-1,與x軸交于A,B兩點,與y軸交于點C,其中A(-3,0)、C(0,-2).查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
 如圖,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于點E,則下列結(jié)論錯誤的是( )
如圖,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于點E,則下列結(jié)論錯誤的是( )| A. | BD+ED=BC | B. | ED+AC>AD | C. | DA平分∠EDC | D. | DE平分∠ADB |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,AB、AC是⊙O的切線,B、C為切點,過點O作AB的平行線交AC于點D,DE⊥AB于點E.
如圖,AB、AC是⊙O的切線,B、C為切點,過點O作AB的平行線交AC于點D,DE⊥AB于點E.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
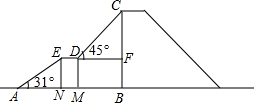 如圖,是某兒童樂園為小朋友設(shè)計的滑梯平面圖.已知BC=5米,AB=8米,中間平臺寬度DE=1米,EN、DM、CB為三根垂直于AB的支柱,垂足分別為N、M、B,∠EAB=31°,DF⊥BC于F,∠CDF=45°.求DM和BC的水平距離BM的長度.(結(jié)果精確到0.1米,參考數(shù)據(jù):sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
如圖,是某兒童樂園為小朋友設(shè)計的滑梯平面圖.已知BC=5米,AB=8米,中間平臺寬度DE=1米,EN、DM、CB為三根垂直于AB的支柱,垂足分別為N、M、B,∠EAB=31°,DF⊥BC于F,∠CDF=45°.求DM和BC的水平距離BM的長度.(結(jié)果精確到0.1米,參考數(shù)據(jù):sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com