
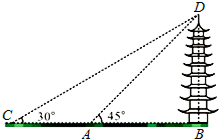
 如圖,某校數學興趣小組的同學欲測量祁陽縣文昌古塔BD的高度,他們先在A處測得古塔頂端點D的仰角為45°,再沿著BA的方向后退12米至C處,測得古塔頂端點D的仰角為30°.求該古塔BD的高度(結果保留根號).
如圖,某校數學興趣小組的同學欲測量祁陽縣文昌古塔BD的高度,他們先在A處測得古塔頂端點D的仰角為45°,再沿著BA的方向后退12米至C處,測得古塔頂端點D的仰角為30°.求該古塔BD的高度(結果保留根號). 分析 先根據題意得出∠BAD、∠BCD的度數及AC的長,再在Rt△ABD中可得出AB=BD,利用銳角三角函數的定義可得出BD的長.
解答 解:根據題意可知:
∠BAD=45°,∠BCD=30°,AC=12m.
在Rt△ABD中,
∵∠BAD=∠BDA=45°,
∴AB=BD.
在Rt△BDC中,
∵tan∠BCD=$\frac{BD}{BC}$,
∴$\frac{BD}{BC}$=$\frac{\sqrt{3}}{3}$,
則BC=$\sqrt{3}$BD,
又∵BC-AB=AC,
∴$\sqrt{3}$BD-BD=12,
解得:BD=6$\sqrt{3}$+6.
答:古塔BD的高度為(6$\sqrt{3}$+6)米.
點評 本題考查的是解直角三角形的應用-仰角俯角問題,涉及到等腰直角三角形的判定與性質、銳角三角函數的定義及特殊角的三角函數值,熟練掌握以上知識是解答此題的關鍵.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
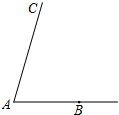 如圖,已知∠CAB,用直尺和圓規(guī)作∠ABD,使∠ABD=$\frac{1}{2}$∠A,射線BD與射線AC相交于點D.(不寫畫法,保留作圖痕跡)
如圖,已知∠CAB,用直尺和圓規(guī)作∠ABD,使∠ABD=$\frac{1}{2}$∠A,射線BD與射線AC相交于點D.(不寫畫法,保留作圖痕跡)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
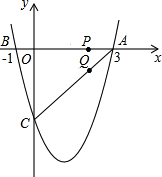 如圖,二次函數y=$\frac{4}{3}$x2+bx+c的圖象與x軸交于A(3,0),B(-1,0),與y軸交于點C.若點P,Q同時從A點出發(fā),都以每秒1個單位長度的速度分別沿AB,AC邊運動,其中一點到達端點時,另一點也隨之停止運動.
如圖,二次函數y=$\frac{4}{3}$x2+bx+c的圖象與x軸交于A(3,0),B(-1,0),與y軸交于點C.若點P,Q同時從A點出發(fā),都以每秒1個單位長度的速度分別沿AB,AC邊運動,其中一點到達端點時,另一點也隨之停止運動.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
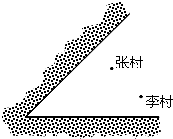 近年來,江蘇省實施“村村通”工程和農村醫(yī)療衛(wèi)生改革,宜興市計劃在某鎮(zhèn)的張村、李村之間建一座定點醫(yī)療站P,張、李兩村坐落在兩相交公路內(如圖所示),醫(yī)療站必須滿足下列條件:①使其到兩公路的距離相等;②到張、李兩村的距離也相等.請你利用尺規(guī)作圖確定P點的位置.(不寫作法,保留作圖痕跡)
近年來,江蘇省實施“村村通”工程和農村醫(yī)療衛(wèi)生改革,宜興市計劃在某鎮(zhèn)的張村、李村之間建一座定點醫(yī)療站P,張、李兩村坐落在兩相交公路內(如圖所示),醫(yī)療站必須滿足下列條件:①使其到兩公路的距離相等;②到張、李兩村的距離也相等.請你利用尺規(guī)作圖確定P點的位置.(不寫作法,保留作圖痕跡)查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com